Cada uma das hastes esbeltas uniformes de massa está soldada na sua extremidade em uma posição tangente à borda do disco circular. O disco gira em um plano horizontal em torno de um eixo vertical fixo por meio do seu centro . Determine as expressões para o momento fletor , a tração , e o cortante transmitido pela solda à haste se o disco possui (a) uma velocidade angular constante em torno de e (b) uma aceleração angular no sentido horário em torno de ao dar a partida. O sentido (SH ou SAH) de faz alguma diferença? Analise apenas as forças no plano horizontal.
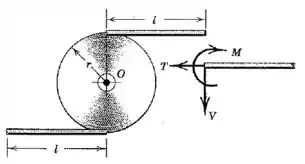
Passo 1
(a) No caso em que o disco possui uma velocidade angular constante, a única aceleração que podemos atribuir ao centro de massa da haste é a centrípeta:
Onde é o raio da trajetória circular do centro de massa da haste (e não da extremidade, portanto esse raio é diferente do raio do disco). Podemos definir um ângulo de forma que:

Então podemos escrever o momento total em relação ao ponto da seguinte forma:
Onde tomamos o componente perpendicular da aceleração centrípeta (a seta azul no desenho), em acordo com a definição de momento.
Passo 2
Ainda falando sobre o caso do item (a), a força é simplesmente a força resultante na direção centrípeta:
E como já vimos no nosso desenho:
E, analogamento, a tração é a força resultante na outra direção, então basta tomar a outra componente da força centrípeta:
E olhando o desenho podemos encontrar uma expressão para o seno:
Então:
Passo 3
(b) Agora vamos tratar do caso em que existe uma aceleração angular no sentido anti-horário, mas com a intenção de calcular , e ao dar a partida.
Vamos refazer o diagrama:
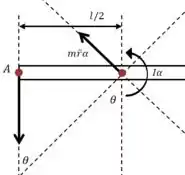
E o momento fletor deve ser igual ao momento associado ao centro de massa da haste, mais o momento associado à tendência da haste de rodar em torno do seu centro de massa:
Sendo que, pelo desenho, podemos determinar que:
Então:
E o momento de inércia da haste é , então:
Passo 4
(c) Agora podemos usar a segunda lei de Newton nas direções normal e tangencial para encontrar as forças e :

Na direção normal (a direção paralela à força ), temos:
E na direção tangencial:
E aqui é mais útil usar a relação :
Resposta
(a) , e .
(b) , e .