Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 152

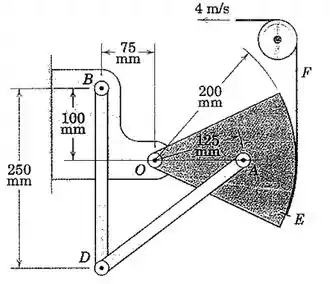
O mecanismo do prob 5/118 é reapresentado aqui, onde a tira flexível F presa ao setor E recebe uma velocidade constante de 4 m/s conforme mostrado. Para o instante em que BD este perpendicular a AO, determine a aceleração angular BD.

Passo 1

Galera, vamos precisar de alguns dados do problema 5/118 para resolver essa questão.

v A = 2,5   m / s

v D = 1,875   m / s

ω A D = 12,5   r a d / s

Agora, vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo.

Bom, agora vamos começar a calcular as acelerações. Pela barra AO, podemos calcular a aceleração de A:

a A = - r A / O ω A O 2 + α A O × r A / O = - v A 2 r A O i ^ + 0

a A = - 50 i ^ m / s 2

Agora, fazemos o mesmo para achar a aceleração de D em relação à barra BD:

a D = - v D 2 r D B j ^ + α B D × r D B = - 1,875 2 - 0,25 j ^ + α B D k ^ × ( - 0,25 j ^ )

a D = 14,06 j ^ + 0,25 α B D i ^   m / s 2

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e D.

a D = a A + a D / A n + a D / A t

Onde:

a D / A n = ω A D × ω A D × r D / A = - 12,5 2 - 0,2 i ^ - 0,15 j ^ = 31,25 i ^ + 23,44 j ^ m / s 2

a D / A t = α A D × r D / A = α A D - 0,2 j ^ + 0,15 i ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

14,06 j ^ + 0,25 α B D i ^ = - 50 i ^ + 31,25 i ^ + 23,44 j ^ + α A D - 0,2 j ^ + 0,15 i ^

Decompondo nas direções, temos o sistema:

0,25 α B D i ^ = - 50 i ^ + 31,25 i ^ + α A D 0,15 i ^

14,06 j ^ = + 23,44 j ^ + α A D - 0,2 j ^

Resolvendo o sistema, temos:

α B D = - 46,9   k ^   r a d / s 2

α A D = 46,9 k ^   r a d / s 2

Resposta

α B D = - 46,9   k ^ r a d s 2

α A D = 46,9 k ^ r a d s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A manivela AB tem uma velocidade angular constante de 1,5 rad/s gira no sentido anti-horário. Para a posição mostrada, determine (a) a velocidade angular da haste BD, (b) a velocidade do colar D.
Sabendo que no instante mostrado a barra AB tem aceleração angular nula e velocidade angular de 15r a d / s no sentido anti-horário, determine (a) a aceleração angular do braço D E , (b) a aceleração
O colar P desliza para fora a uma velocidade relativa constante u ao longo da barra AB, que gira no sentido anti-horário com uma velocidade angular constante de 20r p m . Sabendo que r = 250m m quando
O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é
Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angula