Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 76

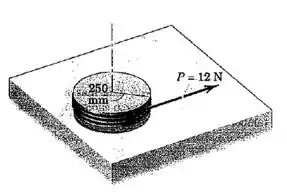
O disco circular maciço de 30   k g está inicialmente em repouso sobre a superfície horizontal, quando uma força P de 12   N , com módulo, direção e sentido constante, é aplicada ao cabo enrolado firmemente em torno de sua periferia. O atrito entre o disco e a superfície é desprezível. Calcule a velocidade angular ω do disco após a força de 12   N ter sido aplicada por dois segundos e determine a velocidade linear do centro do disco após ele ter se deslocado de 1,2 metro a partir do repouso.

Passo 1

Vamos começar calculando a aceleração do centro de massa na direção da força P :

∑ F = m a

12 = 30 a

a = 0,433   m / s 2

E com isso já podemos calcular a velocidade linear desse mesmo centro de massa após um deslocamento de 1,2   m :

v 2 = v 0 2 + 2 a Δ x

O disco parte do repouso, então v 0 = 0 :

v 2 = ( 2 ) ( 0,433 ) ( 1,2 )

v = 1,02   m / s

Passo 2

E agora vamos fazer praticamente a mesma coisa, mas com grandezas angulares. Primeiro vamos encontrar a aceleração angular do disco:

∑ M O = I α

O momento total agindo sobre o disco é o momento da força P , que age a uma distância de 0,250   m do eixo de rotação:

∑ M O = P 0,250 = 12 0,250 = 3   N ∙ m

E o momento de inércia do disco em relação a um eixo perpendicular à superfície é:

I = 1 2 m r 2 = 1 2 30 0,250 2 = 0,9375   k g ∙ m 2

E então a sua aceleração angular é:

α = ∑ M O I = 3 0,9375 = 3,2   r a d / s 2

E assim como antes, podemos calcular a velocidade angular após dois segundos:

ω = ω 0 + α t

E como o disco não tem rotação inicialmente, temos ω 0 = 0 :

ω = 3,2 2 = 6,4   r a d / s

Resposta

A velocidade angular é ω = 6,4   r a d / s , e a velocidade angular é v = 1,2   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra a vista lateral de uma laje de concreto uniforme com uma massa de 12t . A laje está sendo içada lentamente pelo guincho D por meio do cabo preso ao carrinho. Na posição θ = 60 ° , a di
Em uma investigação do “efeito de chicote” resultante de colisões trasieras, a rotação brusca da cabeça é modelada utilizando uma esfera maciça homogênea de massa m e raio r que gira em torno de um ei
O mastro uniforme de 3,6m é articulado à plataforma do caminhão e liberado a partir da posição vertical quando o caminhão parte do repouso com uma aceleração de 0,9m / s 2 . Se a aceleração permanece
A roda desbalanceada possui uma masas de 10k g e rola sem deslizar sobre a superfície horizontal. Quando o centro de massa G passa a linha horizontal através de O como mostrado, a velocidade angular d
A barra esbelta uniforme de massa m e comprimento L , com pequenos roletes nas extremidades, é liberada a partir do repouso na posição mostrada, com o rolete inferior em contato com o plano horizontal