Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 41
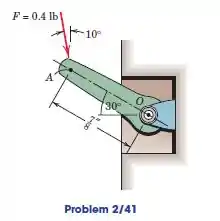
Calcule o momento da força de em relação ao pivô do disjuntor de parede.
Passo 1
Ooi! Vamos lá para a resolução de mais um problema?
Temos uma força e precisamos calcular o momento dela em relação ao ponto . Observe a figura:
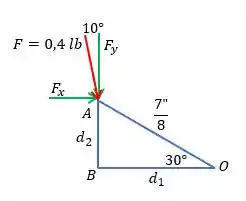
Montamos um triângulo retângulo. A partir dele, e com as informações nos foram fornecidas, vamos encontrar as distâncias e .
Passo 2
Agora vamos calcular as componentes e :
Passo 3
Prontinho, temos as componentes da força e as distâncias, podemos então determinar o momento em relação a .
Considerando o sentido anti-horário como positivo:
no sentido anti-horário.
Resposta
Exercícios de Livros Relacionados
O elemento BD exerce sobre o elemento ABC uma força P dirigida ao longo da linha BD. Sabendo que P deve ter um componente vertical de 1068 N, determine ( a ) a intensidade da força P, ( b ) sua compon
Dois cabos estão ligados juntos em C e carregados como mostra a figura. Sabendo que P = 360 N, determine a tensão a no cabo AC, ( b ) no cabo BC.
Determine a intensidade da força resultante que atua sobre a chapa e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Decomponha F 1 e F 2 em suas componentes x e y .
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.