Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 34
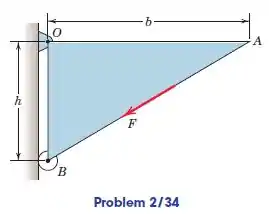
A força de magnitude atua ao longo da borda da placa triangular. Determine o momento de em relação ao ponto .
Passo 1
Olá, tudo bem com você?
Nesse problema, precisamos determinar o momento de em relação ao ponto . Vamos começar ilustrando de uma forma que a compreensão seja fácil.
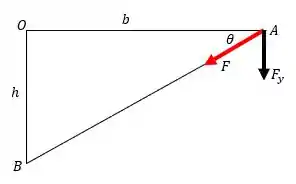
A distância entre o ponto e o ponto é . Vamos considerar o sentindo horário como sendo o positivo.
Veja que, usando o teorema de Pitágoras, podemos determinar a diagonal .
Portanto,
Passo 2
Fazendo as devidas substituições para obter o momento, temos:
Considerando o sentido horário como positivo,
no sentido horário.
Prontinho! Chegamos à solução!
Resposta
Exercícios de Livros Relacionados
Determine a intensidade da força resultante que atua sobre o pino e sua direção, medida no sentido horário a partir do eixo x positivo.
2.33. Se a intensidade da força resultante que atua sobre a argola é 600N e sua direção no sentido horário do eixo x positivo é θ = 30 ° , determine a intensidade de F 1 e o ângulo Φ
2.42. Determine a intensidade e o ângulo medido no sentido anti-horário a partir do eixo y positivo da força resultante que atua no suporte se F B = 600N e θ = 20 °
2.36. Se Φ = 30 ° e F 2 = 3k N , determine a intensidade da força resultante que atua sobre a chapa e sua direção θ, medida no sentido horário a partir do eixo x positivo.
2.41. Determine a intensidade e a direção θ de F B , de modo que a força resultante seja direcionada ao longo do eixo y positivo e tenha uma intensidade de 1500N .