Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 57
A chapa em ângulo reto é fabricada a partir de uma chapa plana com massa por unidade de área e está soldada no eixo horizontal montado no mancal em . Se o eixo é livre para girar, determine a aceleração angular inicial da chapa quando for liberada a partir do repouso com a superfície superior no plano horizontal. Determine também as componentes e da força resultante sobre o eixo em .
Passo 1
Vamos começar encontrando o momento de inércia total do sistema em relação ao eixo .
Onde é o momento de inércia da placa que está na vertical em reção ao eixo . A massa de cada chapa pode ser calculada em função da densidade superficial :
Então:
E para escrever vamos precisar do teorema dos eixos paralelos:
Onde é a distância entre o centro de massa da chapa horizontal e o eixo . Podemos usar o teorema de pitágoras para calcular essa distância:
E então:
De forma que o momento de inércia total é:
E com isso podemos calcular a aceleração angular em torno do eixo :
E a única força que produz momento em torno desse eixo é o peso da placa horizontal (já que a linha de ação do peso da placa vertical atravessa o eixo):
Passo 2
Agora vamos construir um esquema da situação para que possamos aplicar a segunda lei de Newton.
A ideia desse diagrama é representar as acelerações dos centros de massa de cada uma das barras quando o sistema tem aceleração angular em torno do eixo :
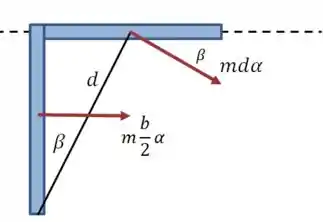
Como a única força que atua na direção da linha pontilhada é , a segunda lei de Newton dá o seguinte resultado:
E podemos calcular através do desenho:
E substituindo :
Passo 3
E ainda aproveitando o mesmo desenho, vamos considerar a segunda lei de Newton na direção do eixo (a vertical no desenho).
As forças que agem nessa direção são e os dois pesos, e a única aceleração resultante é a outra componetne da aceleração do centro de massa da chapa horizontal:
E pelo desenho é fácil ver que , então:
E substituindo :
Resposta
A aceleração angular inicial é . As componentes da força são e .