Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 58
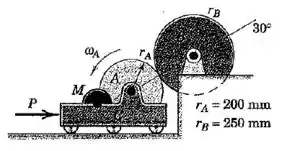
O disco possui uma massa de e um raio de giração centroidal de . A unidade de potência é composta por um motor e um disco em , que é acionado a uma velocidade angular constante de . Os coeficientes de atrito estático e dinâmico entre os dois discos são e , respectivamente. O disco está inicialmente parado quando o contato com o disco é estabelecido pela aplicação da força constante . Determine a aceleração angular de e o tempo necessário para atingir sua velocidade de regime permanente.
Passo 1
Vamos começar olhando para o carrinho de baixo (a unidade de potência ), e aplicando a segunda lei de Newton na direção horizontal:
Além da força que o empurra para a direita, temos a força do contato entre os discos e a força de atrito também nesse contato:
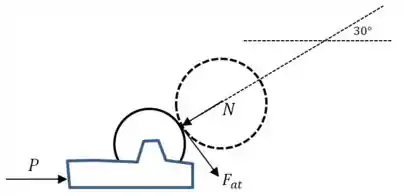
Passo 2
E a força que gera momento sobre o disco é a força de atrito:
Que age a uma distância do centro do disco, então o momento é:
Onde é o raio de giração do disco :
Passo 3
Agora queremos saber quanto tempo a roda leva para atingir sua velocidade de regime permanente.
Nós já sabemos que a aceleração transmitida é de , então só precisamos saber qual é a velocidade de regime permanente para calcular o tempo necessário.
Já que as rodas estão em contato, as suas velocidades sempre obedecem à seguinte relação:
Onde convertemos a velocidade angular dada em rotações por minuto para radianos por segundo:
E o tempo necessário para acelerar a roda até essa velocidade, partindo do repouso, pode ser calculado com a seguinte equação:
Resposta
A aceleração angular é , e o tempo necessário é .