Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 55
O cilindro de kg sustentado pelos suportes dos mancais em e tem um momento de inércia em relação ao eixo vertical por meio de seu centro de massa igual a . O disco e os suportes têm um momento de inércia em relação ao eixo vertical de rotação igual a . Se um torque é aplicado ao disco por meio de seu eixo, com o disco inicialmente em repouso, calcule as componentes horizontais das forças suportadas pelos mancais em e .
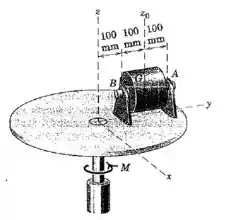
Passo 1
Queremos escrever equações para a força e o momento resultante que agem sobre esse sistema, mas para isso precisamos calcular a aceleração angular:
Onde é o momento de inércia do sistema em relação ao eixo , e é o momento total aplicado sobre o eixo.
O momento de inércia do disco e do suporte já foi dado em relação ao eixo , mas precisamos usar o teorema dos eixos paralelos para calcular o do cilindro, que foi dado em relação a :
Onde é a distância entre o eixo e o eixo :
E com isso podemos calcular a aceleração angular no caso em que um momento é aplicado sobre o eixo:
Passo 2
Beleza, agora já podemos calcular a aceleração do centro de massa do cilindro, e com isso escrever algumas equações para a força resultante sobre o cilindro.
Começando pela componente tangencial:
Como o cilindro está a do centro de um disco girando com aceleração angular , a sua aceleração tangencial é:
E as únicas forças que movem o cilindro na direção tangencial são justamente as duas componentes horizontais de e que queremos calcular:
Passo 3
E agora vamos escrever uma equação para o momento resultante agindo sobre o centro de massa do cilindro
E agora temos que escrever os momentos das forças agindo sobre o cilindro:
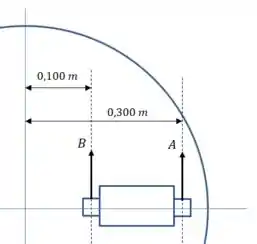
E então:
Agora ficamos com um sistema de duas equações:
Vamos multiplicar a equação de cima por :
E agora subtrair a segunda da primeira:
E substituindo em qualquer uma das duas, encontramos que:
Resposta
As componentes horizontais das forças são e .