Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 23
A chapa retangular é submetida a deformação mostrada. Determine a deformação por cisalhamento média da chapa
.
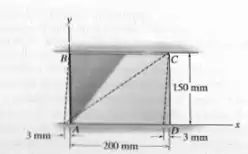
Passo 1
Podemos calcular o ângulo de giro pela seguinte relação:
Passo 2
Podemos então calcular a deformação por cisalhamento:
Resposta
Exercícios de Livros Relacionados
Um vaso esférico de pressão de 500 m m de diâmetro interno deve ser fabricado com um aço cuja resistência última à tração é de 400M p a . Sabendo-se que a máxima pressão deve ser de 8,3M p a e que um
Um vaso esférico de pressão de 500 m m de diâmetro interno e 6,35 m m de espessura da parede é fabricado com um aço cuja a tensão última de tração é de 400M p a . Determinar o coeficiente de segurança
6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec
6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.
6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec