Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 151
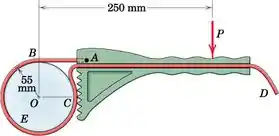
A chave de banda é útil para afrouxar e apertar itens como o filtro de água para toda a casa E mostrado. Suponha que os dentes da chave não escorreguem na banda no ponto C e que a banda esteja frouxa de C até sua extremidade D. Determine o coeficiente mínimo de atrito estático para o qual a banda não escorregará em relação ao filtro fixo.
Passo 1
Ao assumir que a tensão T2 é maior que T1, podemos escrever a expressão
Podemos ver no esboço abaixo que o ângulo é
Portanto, a expressão para a tensão T2 é agora
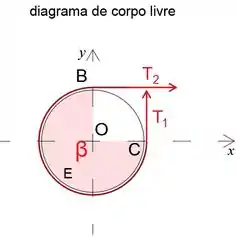
Passo 2
A seguir, desenharemos o diagrama de corpo livre do cabo com a força aplicada P, a tensão do cabo T2 e as forças de reação em C atuando nele
Ao igualar a soma das forças na direção y a zero, determinaremos a força de atrito FC
Equacionando a soma dos momentos sobre o ponto C a zero, determinaremos a tensão T2
Passo 3
Equacionando a soma das forças na direção x a zero, determinaremos a força de reação normal NC
A seguir, vamos analisar a tensão no cabo logo acima do ponto C
Teremos a tensão do cabo atuará na guerra, enquanto a força de fricção do filtro FF atuará na direção oposta
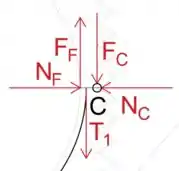
Passo 4
Ao igualar a soma das forças na direção x a zero, determinaremos a força de reação normal NF
Uma vez que precisamos determinar o atrito estático mínimo, vamos assumir que a força FF é a força de atrito máxima
Ao igualar a soma das forças na direção y a zero, escreveremos a expressão para a tensão T1
Vamos substituir FF por e FC por P
Finalmente, uma vez que escrevemos a expressão para a tensão T1, e já determinamos a tensão T2, podemos substituir T1 pela expressão (2) e T2 por seu valor na equação (1)
Podemos dividir os dois lados da equação por P
Passo 5
Usando uma calculadora gráfica como o Desmos (link nos comentários), plotaremos a função à direita e simplesmente leremos para o valor de 3,545
