Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 87
Determine a área da superfície interna (gerada girando ABC completamente em torno do eixo z) do corpo mostrado na seção transversal.
Passo 1
Usando o teorema de Pappus, podemos escrever a expressão para a área do corpo como
Onde x ‾ é o centróide das linhas, L é o comprimento das linhas e θ ângulo de rotação
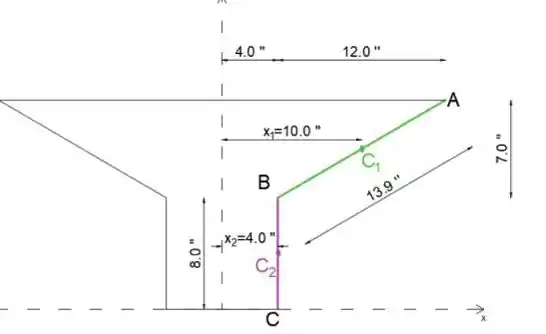
Podemos ver no esboço as seguintes dimensões:
Uma vez que os comprimentos das partes 1 e 2 são
E ângulo da rotação é
Passo 2
Coloque na expressão (1)
A área da superfície total
Resposta
Exercícios de Livros Relacionados
Um cotovelo para o duto de ventilação é feito de chapa metálica de espessura uniforme. Determine o centro de gravidade do cotovelo.
Determine o centro de gravidade mostrado na figura, sabendo que ela é feita de barras finas de latão o diâmetro uniforme.
Um duto cilíndrico de 200m m de diâmetro e um duto retangular de 100 × 200m m devem ser unidos tal como indica a figura. Sabendo que os dutos são fabricados a partir da mesma chapa de metal, que tem e
A estrutura de uma estufa de plantas é construída a partir de tubos uniformes de alumínio. Determine o centro de gravidade da parte da estrutura mostrado na figura
Determine o centro de gravidade mostrado na figura, sabendo que ela é feita de barras finas de latão o diâmetro uniforme.