Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 105
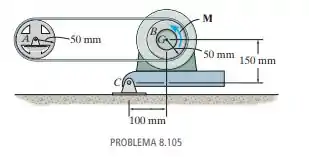
Um motor de tem um centro de gravidade em e está conectado por um pino em C para manter uma tração pré-tensionadora na correia propulsora. Determine o menor torque M em sentido anti-horário que precisa ser fornecido pelo motor para girar o disco B se a roda A travar e fizer com que a correia deslize sobre o disco. Não há deslizamento em A. O coeficiente de atrito estático entre a correia e o disco é .
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Sabemos que o peso do motor causa um atrito com a correia. Este atrito é responsável por não deixar o disco girar. Logo, a força de atrito é dada por:
Logo, esta força vai gerar um momento dado por:
Este momento deve ser pelo menos igual ao momento aplicado:
Resposta
Exercícios de Livros Relacionados
Sabendo que é necessário um torque de intensidade 30N ⋅ m para iniciar a rotação do eixo vertical, determine o coeficiente de atrito estático entre as superficies anelares de contato.
Sabendo que o coeficiente de atrito estático é 0,30 e que o tambor de freio está rodando no sentido anti-horário, determine o mínimo valor de a para o qual o freio não é autotravante.
Um cabo passa em torno de três tubos paralelos. Dois dos tubos são fixos e não podem rodar, enquanto o terceiro tubo é girado vagarosamente. Sabendo que os coeficientes de atrito são μ s = 0,25 e μ k
A velocidade de um tambor de freio mostrado na figura é controlada por uma cinta fixada a uma cinta fixada a uma barra de controle A D . A força P de intensidade de 110N é aplicada na barra de control
Um cabo passa em torno de três tubos paralelos. Sabendo que os coeficiente de atrito são μ s = 0,25 e μ k = 0,20 , determine (a) o menor peso W para o qual o equilibrio é mantido, (b) o maior peso W q