Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 60
O dispositivo robótico é composto pela base estacionária , o braço articulado em , e o braço articulado em . Os eixos de rotação são perpendiculares ao plano da figura. Calcule (a) o momento aplicado ao braço , necessário para girá-lo em torno da articulação a no sentido anti-horário a partir da posição mostrada, com a articulação travada e (b) o momento aplicado ao braço necessário para girá-lo em torno da articulação na mesma taxa, com a a articulação travada. A massa do braço é de e a de é de , com a parte estacionária da articulação totalmente excluída e a massa da articulação dividida igualmente entre os dois braços. Assuma que os centros de massa e estão nos centros geométricos dos braços e modele os braços como hastes esbeltas.
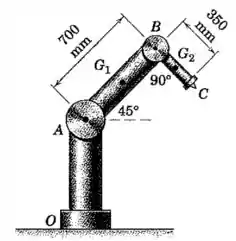
Passo 1
(a) Para encontrar a aceleração angular, sempre vamos partir da seguinte fórmula:
No primeiro item precisamos calcular o momento de inércia dos dois braços ( e ) em relação a um eixo perpendicular ao plano da página e que passa pelo ponto .
A do braço é mais fácil, pois podemos simplesmente usar a fórmula tabelada:
Mas para o braço , precisamos usar o teorema dos eixos paralelos:
Onde e é a distância entre e :
Então:
Passo 2
Agora que temos o momento de inércia, fica faltando apenas calcular o momento total em relação ao mesmo ponto .
Além do momento mencionado no enunciado, teremos os momentos dos pesos de cada braço.
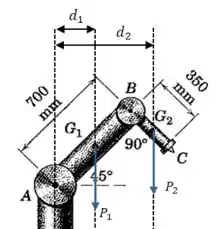
E então:
Passo 3
(b) Agora vamos fazer uma conta parecida para o momento aplicado ao braço com a articulação travada.
O momento de inércia do braço em relação a um eixo perpendicular ao plano da página, e que passa pelo ponto é:
Então:
E novamente, temos o momento aplicado sobre o braço e o momento do peso :
Resposta
(a) .
(b) .