Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 72
Classifique cada uma das estruturas mostradas nas figuras como complenamente, parcialmente ou impropriamente vinculada, se completatamente vinculada, classifique-a também como determinada ou indeterminada. (Todos os elementos podem atuar tanto sob tração como sob compressão.)
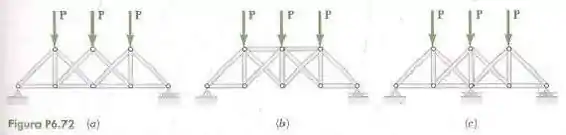
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para este tipo de problema podemos seguir um passo a passo para melhorar a organização. Vamos determinar o número de membros , o número de nós e a quantidade de reações dos vínculos .
Determinando esses parâmetros podemos definir nossa estrutura a partir das seguintes relações:
Passo 2
Para a letra temos que:
No caso temos que:
Portanto, para o caso em questão, a estrutura é parcialmente vinculada.
Passo 3
Para a letra temos que:
No caso temos que:
Se aplicarmos as relações de estática para determinar as reações, veremos que é possível encontra-las, logo, essa estrutura é completamente vinculada e determinada.
Passo 4
Para a letra temos que:
No caso temos que:
Portanto, para o caso em questão a estrutura é completamente vinculada e indeterminada.