Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 43
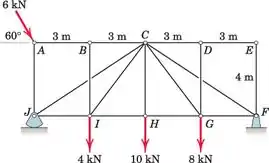
Os membros CJ e CF da treliça carregada cruzam mas não estão ligados aos membros BI e DG. Calcular as forças nos membros BC, CJ, CI e HI.
Passo 1
E ai gurizada tudo certo? O enunciado pede que a gente calcule as forças nos membros BC, CJ, CI e HI.
Se passarmos uma seção pelos membros BC, BH e AH e analisarmos a parte da treliça à esquerda, notaremos que existem cinco forças desconhecidas atuando (BC, BH, AH, AX e AY), portanto, devemos determinar forças de reação em A do diagrama de corpo livre
Passo 2
Uma vez que esta treliça é um pouco complicada, vamos isolar a treliça e determinar as forças de reação do diagrama de corpo livre
Passo 3
Agora que determinamos as forças de reação em A, podemos passar uma seção pelos membros AB, CJ e IJ e analisar a porção da treliça à esquerda
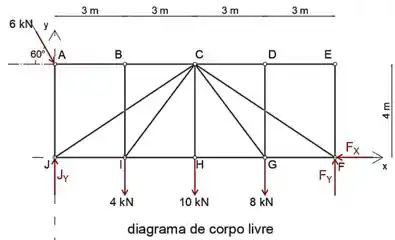
Ao igualar a soma dos momentos sobre o ponto C a zero, eliminaremos as forças AB e CJ, para que possamos determinar a força no membro IJ
Vamos supor que todos os membros estão em tensão
Passo 4
Ao igualar a soma das forças na direção y a zero, a força CJ será a única incógnita na equação
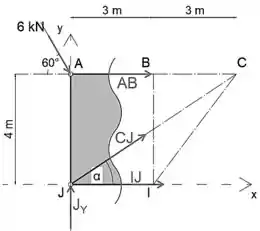
O ângulo que o membro CJ faz com o eixo x é
Passo 5
Obtivemos resultado negativo, o que significa que o membro CJ está em compressão
O mais fácil, portanto, também a maneira mais rápida de determinar a força AB é igualar a soma dos momentos sobre o ponto J a zero
Passo 6
Ao analisar a junta B, podemos determinar as forças nos membros BC e BI
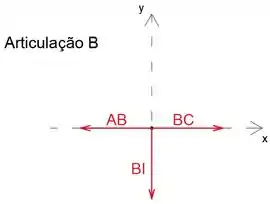
Passo 7
Finalmente, analisando a junta I, podemos determinar as forças nos membros Cl e Hl
Observe que o ângulo que o membro CI machos com eixo x é
