Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 36
Determine as forças nos membros BC, CF e EF da treliça carregada.
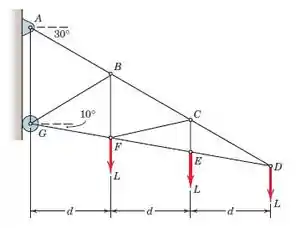
Passo 1
Primeiro, vamos dar uma olhada em alguma geometria. O ângulo entre AB e AG é 60∘. O triângulo AGD nos dá o ângulo entre CD e DE-20 ∘. Podemos projetar AB, BC e CD na horizontal e obtemos d. Sabendo o ângulo entre a horizontal e eles, 30∘, podemos obter que seu comprimento é . Se projetarmos DE, EF e FG na horizontal, obteremos d. Com o mesmo processo, obtemos seu comprimento-1.015d. Por simetria, sabemos que os ângulos entre AB, BC e CD com a horizontal devem ser iguais a 60 ∘. Agora olhe para o triângulo CDE. Temos que encontrar o comprimento do membro CE. Podemos fazer isso com a lei dos senos.
O próximo ângulo entre CE e EF é 80 ∘ visto que o ângulo entre CE e DE é 100 ∘. Com a lei do cosseno, podemos obter o comprimento de CF.
Passo 2
Agora, com a lei dos senos, podemos obter o ângulo entre CF e CE.
Finalmente, podemos começar a resolver o problema cortando os membros BCCE e CF Olhando para o momento de todas as forças externas sobre o ponto C, obtemos:
Passo 3
EF tem que ser compressão para que isso seja verdade. O próximo momento de todas as forças externas sobre D nos dá:
CF tem que ser compressão para que isso seja verdade. Momento sobre E:
BC tem que haver tensão para que isso seja verdade.