Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 45
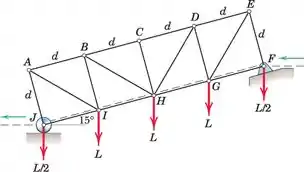
A treliça suporta uma rampa (mostrada com uma linha tracejada) que se estende de um nível de aproximação fixo próximo à junta F até um nível de saída fixo próximo a J. As cargas mostradas representam o peso da rampa. Determine as forças nos membros BH e CD.
Passo 1
Primeiro, temos que calcular a força de reação no ponto F, mas como a situação é simétrica, essa força de reação será igual àquela em J.
Momento sobre J de todas as forças externas:
Passo 2
A força de reação aponta para cima, então a soma da força no ponto F é 1.5L.
Agora cortamos CD, DH e GH.
Olhando para o momento sobre o ponto G e o ponto F, podemos obter duas equações:
Subtraindo-os, obtemos:
Passo 3
O sinal de menos está ali porque a força real é oposta à que previmos.
Retornando ao nosso momento de forma de equação anterior sobre G, obtemos:
Como a treliça é simétrica, os membros DH e BH estão fazendo a mesma coisa, eles são iguais.