Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 26
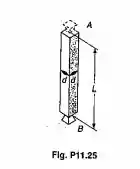
Uma coluna de aço biarticulada, de 100x100m de seção transversal é apoiada como mostrado no Prob. 11.25. Sabendo-se que inicialmente a força na coluna é zero, determinar o comprimento L necessário, se a flambagem deve ocorrer para um aumento de temperatura de 25 Usar E=200GPa e =11,7x10^-6/.
3
Passo 1
Faala aí, se você veio após o problema anterior já conhece como funciona aqui. Se não veio temos uma flambagem causada por variação de temperatura. Vou te explicar direitinho aqui a gente precisa encontrar uma relação entre L e a galera que a gente conhece que nos foi fornecida no enunciado então bora pra análise.
A coluna inicialmente não tinha nenhuma força aplicada mas ao receber um incremento de temperatura sofre flambagem. O que rolou aqui foi o seguinte, a coluna foi aquecida e se dilatou, lembra lá da física? Essa dilatação térmica gerou um deslocamento axial .
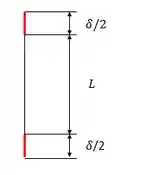
Porém os apoios não permitem que isso aconteça e reagiram ao deslocamento com um esforço axial para deslocar o mesmo no sentido oposto, o que provocou a flambagem.
Se esse peso indicado na figura é o que causa a flambagem podemos dizer que:
Com isso podemos usar a fórmula da dilatação linear e relacionar o comprimento L que a gente quer com todos os dados que a gente tem.
Passo 2
Vamos a fórmula da dilatação linear, temos que:
Onde é o comprimento inicial da coluna, é o coeficiente de dilatação térmica e é a variação de temperatura.
A gente tem também do deslocamento axial que:
E como foi falado os apoios não permitem deslocamento sendo assim, os dois deslocamentos são idênticos um tenta expandir e o outro comprime e assim:
Rearrumando:
Onde:
E
Substituindo:
Ainda não terminado precisamos abrir a fórmula do peso crítico para encontrar uma relação que nos dê em função da galera que a gente tem.
Passo 3
A fórmula do peso crítico é dada por:
Nesse caso de seção quadrada temos:
Daí fica:
Voltando a nossa equação:
Substituímos o peso crítico e enfim encontramos a relação em que todos os dados são conhecidos.
Isolando L, temos:
E substituindo:
Temos:
E aí:
E em metros: