Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 66
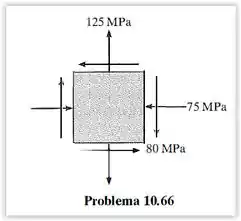
As componentes do estado plano de tensão em um ponto crítico de uma carcaça de aço estrutural são mostradas na figura. Determine se ocorreu falha (escoamento) com base na teoria da energia de distorção máxima.
Passo 1
O problema pede que determinemos se ocorreu escoamento em uma carcaça de aço estrutural com base na teoria da energia de distorção máxima. Vamos ao dados:
Para resolver esse problema basta calcular as tensões principais e depois fazer a verificação usando a teoria da energia de distorção máxima.
Passo 2
Calculando as tensões principais:
Passo 3
Encontramos as tensões principais! Agora vamos verificar se ocorreu escoamento.
O resultado foi menor que , portanto, de acordo com a teoria da energia de distorção máxima, o material não escoa.
Resposta
O material não escoa.