Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 101

Um elemento diferencial é submetido à deformação no plano que tem as seguintes componentes: ∈ x = 950 × 10 - 6 , ∈ y = 420 × 10 - 6 ,   γ x y = - 325 × 10 - 6 . Use as equações de transformação da deformação e determine (a) as deformações principais e (b) a deformação por cisalhamento máxima no plano e a deformação média associada. Em cada caso, especifique a orientação do elemento e mostre como as deformações distorcem o elemento.

Passo 1

Fala aí pessoal. Vamos, primeiramente, determinar as deformações principais no ponto A. Primeiro, vamos calcular a deformação média:

∈ m é d = ( ∈ x + ∈ y ) 2

Substituindo, teremos:

∈ m é d = 685 × 10 - 6

Este será o centro do círculo. Agora, vamos calcular o raio deste:

R = ∈ m é d 2 + γ x y 2 2

Substituindo, teremos:

R = 310,856 × 10 - 6

Para as deformações principais, basta somar e diminuir o raio da tensão média, ficando com:

∈ 1 = 996 × 10 - 6

∈ 2 = 374 × 10 - 6

O problema também nos pede para especificar a orientação dos elementos. Sabemos que:

t g 2 θ = γ x y ( ∈ x - ∈ y )

Logo, temos que:

θ p 1 = - 15,8 °

θ p 2 = 74,2 °

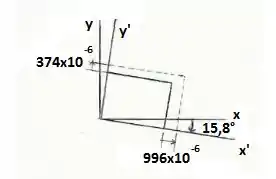
Passo 2

A letra b nos pede a deformação máxima no plano e a deformação média associada. Sabemos que elas serão dadas por:

∈ m é d = ( ∈ x + ∈ y ) 2

γ m á x 2 = ∈ m é d 2 + γ x y 2 2

Logo, substituindo, ficaremos com:

∈ m é d = 685 × 10 - 6

γ m á x = 622 × 10 - 6

O problema também nos pede para especificar a orientação dos elementos. Sabemos que:

t g 2 θ = γ x y ( ∈ x - ∈ y )

Logo, temos que:

θ s 1 = 29,2 °

θ s 2 = 119 °

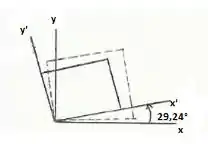
Resposta

  1. ∈ 1 = 996 × 10 - 6 ; ∈ 2 = 374 × 10 - 6 ; θ p 1 = - 15,8 ° ; θ p 2 = 74,2 °
  2. ∈ m é d = 685 × 10 - 6 ;   γ m á x = 622 × 10 - 6 ; θ s 1 = 29,2 ° ; θ s 2 = 119 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 10.69 usando a teoria da tensão de cisalhamento máxima. As duas tensões principais têm sinais opostos.
As componentes de deformação no ponto A sobre a carcaça são ∈ x = 250 × 10 - 6 , ∈ y = 400 × 10 - 6 ,γ x y = 275 × 10 - 6 ,∈ z = 0 . Determine (a) as deformações principais em A, (b)a deformação por c
A viga de alumínio tem seção transversal retangular mostrada na figura. Se for submetida a um momento fletor M=7,5k N . m , determine o aumento na dimensão de 50 mm na parte superior da viga e a reduç
A roseta de deformação a 60 ° está montada sobre uma viga. As seguintes leituras foram obtidas para cada extensômetro: ϵ a = 600 ( 10 - 6 ) , ϵ b = - 700 ( 10 - 6 ) , ϵ c = 350 ( 10 - 6 ) . Determine