Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 104

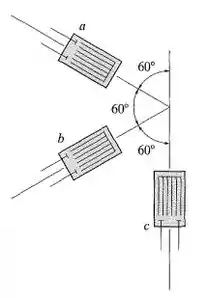
A roseta de deformação a 60 ° está montada sobre uma viga. As seguintes leituras foram obtidas para cada extensômetro: ϵ a = 600 ( 10 - 6 ) , ϵ b = - 700 ( 10 - 6 ) , ϵ c = 350 ( 10 - 6 ) . Determine ( a ) as deformações principais no plano e suas orientações e ( b ) a deformação por cisalhamento máxima no plano e a deformação normal média. Em cada caso, mostre o elemento distorcido devido a essas deformações.

Passo 1

a) Fala galera, bora pra mais um problema de Resmat. O problema quer que a gente determine as deformações principais no plano.

Primeiro, temos que as deformações dadas pelos extensômetros são:

ℇ a = 600 × 10 - 6 → θ a = 0 ° ℇ b = - 700 × 10 - 6   → θ b = 60 ° ℇ c =   350 × 10 - 6 → θ c = 120 °

Repara que nosso eixo x   do nosso referencia está na direção a .

Podemos usar essas fórmulinhas para achar as deformações nos nossos eixos:

ℇ x = ℇ a ∴ ℇ x = 600 × 10 - 6

ℇ y = 1 3 2 ℇ b + 2 ℇ c - ℇ a ∴ ℇ y = - 433,33 × 10 - 6

γ x y = 2 3 ℇ b - ℇ c = - 1212,44 × 10 - 6

Aí com isso a gente consegue achar as principais. Vem!

Passo 2

Para calcularmos as deformações principais vamos usar a seguinte fórmula:

ℇ 1,2 = ℇ x + ℇ y 2 ± ℇ x - ℇ y 2 2 + γ x y 2 2

Subsituindo, ficamos com:

ϵ 1,2 = 600 × 10 - 6 + - 433,33 × 10 - 6 2 ± 600 × 10 - 6 - - 433,33 × 10 - 6 2 2 + - 1212,44 × 10 - 6 2 2

Onde teremos:

ℇ 1 = 880 × 10 - 6 ℇ 2 = - 713 × 10 - 6

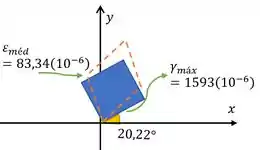
Passo 3

A sua orientação será dada por:

t g   2 θ p = γ x y ℇ x - ℇ y

t g   2 θ p = - 1212,44 600 + 433,33

θ p 1 = - 24,78 °

θ p 2 = - 24,78 ° - 90 °

θ p 2 = - 114,78 °

Aí fazendo o desenho disso bem bonito:

Passo 4

b) Aí bora achar a deformação por cisalhamento máxima no plano e a deformação normal média, que ele pede também.

Só usar essas fórmulinhas:

γ m á x = 2 ℇ x - ℇ y 2 2 + γ x y 2 2 = 2 600 × 10 - 6 - - 433,33 × 10 - 6 2 2 + - 1212,44 × 10 - 6 2 2

γ m á x 1593 × 10 - 6

ℇ m é d = ℇ x + ℇ y 2 = 83,34 × 10 - 6

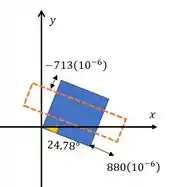
Passo 5

A sua orientação será dada por:

t g   2 θ s = - ℇ x - ℇ y γ x y = - 600 × 10 - 6 - - 433,33 × 10 - 6 - 1212,44 × 10 - 6

θ s = 20,22 °

Aí fazendo o desenho disso bem bonito:

Resposta

ℇ 1 = 880 × 10 - 6   ℇ 2 = - 713 × 10 - 6

γ m á x = 1593 × 10 - 6

ℇ m é d = 83,34 × 10 - 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As componentes do estado plano de tensão em um ponto crítico sobre uma carcaça fina de aço são mostradas na figura. Determine se ocorre falha (escoamento) com base na teoria da tensão de cisalhamento
O elemento está sujeito às tensões mostradas na Figura. Se σe = 350 MPa, determine o fator de segurança para essa carga com base na (a) teoria da tensão de cisalhamento máxima e (b) teoria da energia
Deduza uma expressão para um torque equivalente M e que, se aplicado sozinho a uma barra maciça de seção transversal circular, provocaria a mesma energia de distorção que a aplicação combinada de um m
O resultado do cálculo das cargas internas em uma seção crítica ao longo do eixo de acionamento de aço de um navio são um torque de 3,45 kN.m, um momento fletor de 2,25 kN.m e uma propulsão axial de 1
As componentes do estado plano de tensão em um ponto crítico sobre uma carcaça fina de aço são mostradas na figura. Determine se ocorre falha (escoamento) com base na teoria da energia de distorção má