Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 22
O comprimento original da mola de módulo é . Determine os componentes e da força que a mola exerce no pino , quando ele está na posição . (A força em uma mola é dada por , onde é o alongamento da mola em relação ao seu comprimento original.)
Passo 1
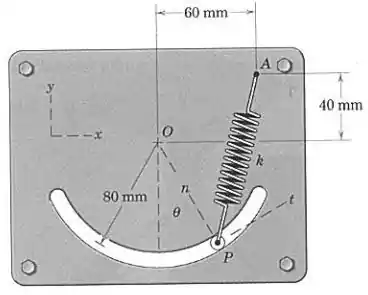
Pessoal, primeiro vamos determinar o vetor unitário , que vai de para . Pela figura, vemos que as coordenadas do ponto em relação à origem são e as do ponto são , tudo em milímetros.
Então, quando , temos:
Passo 2
Agora vamos calcular o módulo da força na mola:
onde e é a diferença entre o comprimento final e o comprimento original da mola, em metros:
Passo 3
Como já temos o módulo da força e o vetor unitário na mesma direção e sentido em que essa força atua, podemos escrever:
Logo,
Resposta
Exercícios de Livros Relacionados
Determine as componentes x e y de cada força que atua sobre a chapa de fixação de uma treliça de ponte. Mostre que a força resultante é zero.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Determine a intensidade e a direção θ da força resultante F R . Expresse o resultado em termos das intensidades das componentes F 1 e F 2 e do ângulo ϕ .
Expresse cada uma das três forças que atuam sobre o suporte na forma vetorial cartesiana e determine a intensidade da força resultante e sua direção, medida no sentido horário a partir do eixo x posit
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.