Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 138
138- A estrutura mostrada está sendo considerada como parte de um grande vaso cilíndrico que deve suportar cargas externas. A instrumentação com extensômetros indica que a força compressiva no elemento vale . Determine as forças nos elementos e . Faça uso da simetria.
Passo 1
Pelo dado da questão temos:
E pela simetria podemos dizer:
E antes de analisar a junta e a junta para saber as forças nas barras nós precisamos dominar a geometria do triângulo .
Pela lei dos cossenos nós temos que:
E pela lei dos senos temos:
Fazendo separadamente os dois ângulos nós encontramos:
Passo 2
Com isso teremos as seguintes forças na junta .
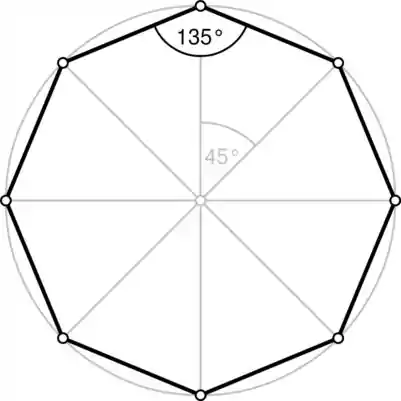
está a do eixo pois ele respeita a geometria do octógono regular que tem de ângulo interno. Tal como a fórmula da soma dos ângulos internos:
Com o sentido da força entrando no nó temos que a compressão terá sinal positivo
Então fazendo a soma das forças verticais nós teremos:
Como
Temos:
Força trativa.
Passo 3
Agora para a junta .
Onde rotacionamos o círculo para a direita em graus e encontramos os ângulos simétricos para a força entre já para as forças impera o raciocínio do ângulo formado no octógono assim como na questão passada.
Fazendo então a soma das forças verticais teremos:
O que é uma força compressiva.