Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 57a
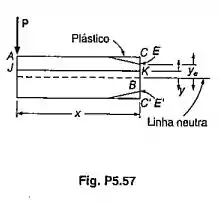
Considerar a viga em balanço AB discutida na Sec 5.10 e a porção ACKJ da vga, que está localizada à esquerda da seção transversal CC’ e acima do plano horizontal JK onde K é um ponto a uma distancia acima da linha neutra (veja a figura). Pede-se (a) Lembrando que entre C e E e entre E e K, mostrar que a intensidade da força cisalhante horizontal H exercida na face inferior da porça da viga ACKJ é
(b) Observando que a tensão de cisalhamento em K é:
E lembrando que é uma função de definida pela Eq. 5.18, desenvolver também a equação
Passo 1
Vamos começar lembrando que a tensão é força sobre área. Então, se dividirmos uma força por uma área termos a tensão:
Se a gente olhar pra seção transversal, a gente vai ver que a base é contante. Então a área é:
Logo:
Então pra encontrar a força basta integrar:
Passo 2
Ok, essa parte você já sabia. A o pergunta aqui é: Qual é o comportamento da função ?
Como estamos trabalhando com uma deformação plástica, o comportamento da tensão não é fácil de prever.
Mas não se procupe, se a gente lê com atenção o texto da questão, vamos encontrar a resposta. A questão diz: “Lembrando que entre C e E e entre E e K”; Então:
Passo 3
Beleza, agora é so integrar a equação considerando os intervalos.
O nosso intervalo parte de um ponto na zona elástica, passa pela zona plástica, e vai até o topo da viga.
E concluímos nossa demonstração:
Resposta
Ei, a resposta está no passo a passo :)