Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 143
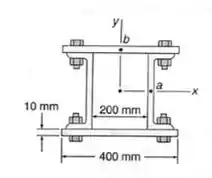
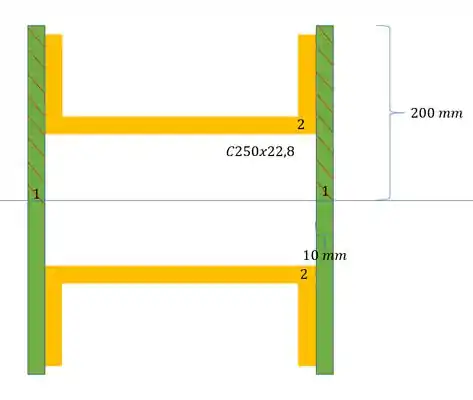
Uma coluna é fabricada aparafusando-se firmemente dois perfis laminados a duas placas, como mostrado. Determinar a tensão de cisalhamento no ponto , causada por uma força cortante de , aplicada ao longo do eixo .
Passo 1
Fala ai pessoal, nosso objetivo aqui é determinar a nossa máxima tensão cisalhante, que ocorre no ponto . Sabemos que no pilar vamos ter que calcular a tensão pela seguinte equação.
- Tensão cisalhante devido o cortante
Em que:
Sabemos que a máxima tensão cisalhante vai ocorrer onde a LN passa, como a nossa seção é simétrica, sabemos que será bem no eixo de simetria, bem no ponto , como os perfis estão ligados por uma chapa, precisamos usar o dobre da espessura, ou seja:
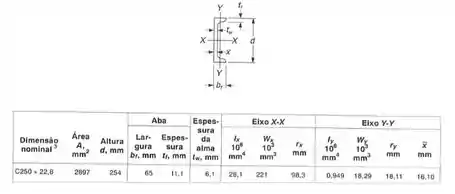
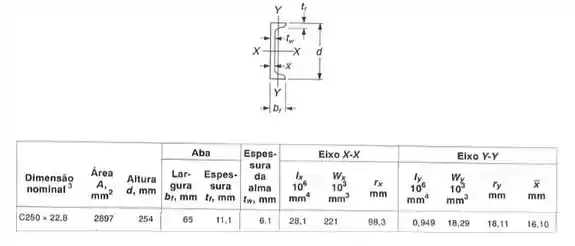
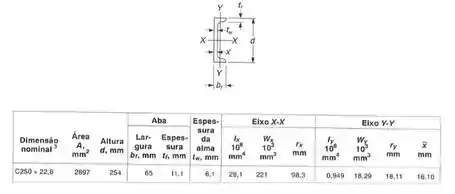
Como o nosso perfil é dado por:
Podemos ter os seguintes dados pela tabela:
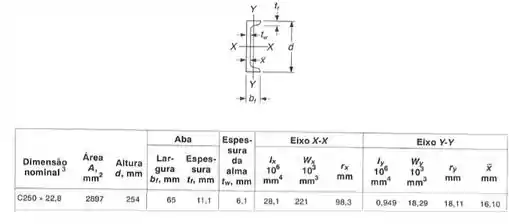
E veja o seguinte, para fazermos a conta tranquilo, é só virarmos a seção e fazermos a mesma conta, porque com ela virada fica fácil de visualizar.
Passo 2
Vamos determinar primeiro o momento de inércia, já que temos que usar ele nas duas fórmulas. O nosso passo a passo é:
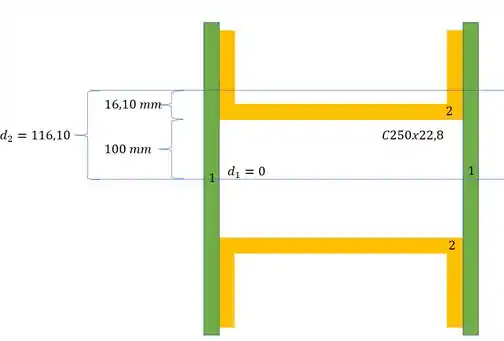
- Primeiro determinamos uma divisão em seções mais simples
- Em segundo determinamos as áreas de cada uma das seções mais simples:
- Em terceiro, determinamos a distância do centroide mais simples para a LN:
- Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:
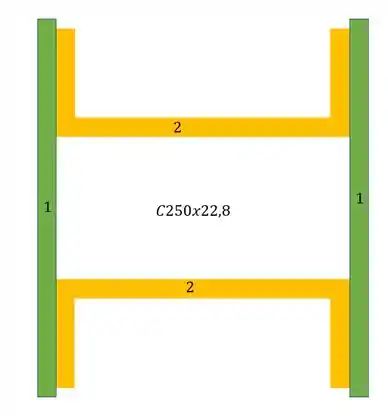
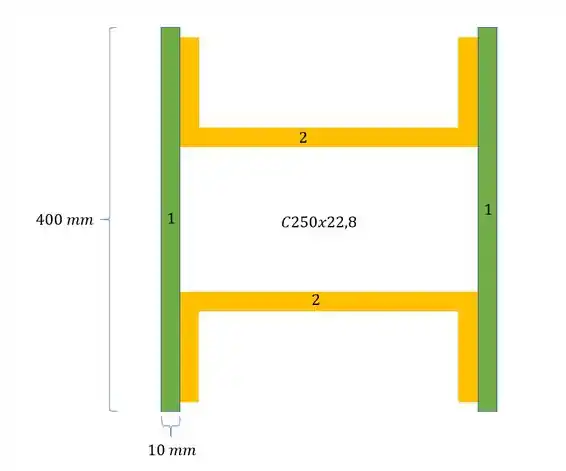
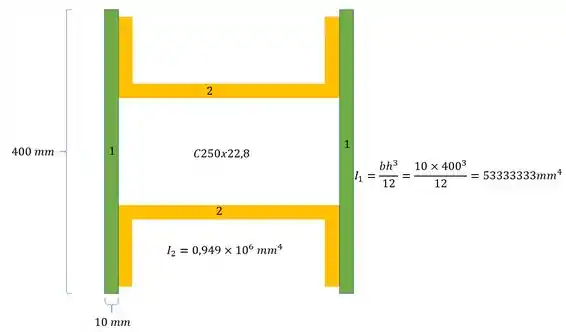
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Passo 3
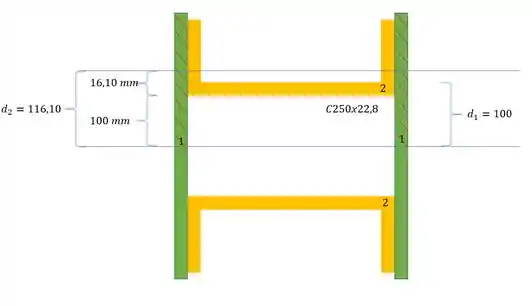
Para o momento estático, da tensão cisalhante, precisamos determinar os seguintes dados:
- Ponto central onde passa a LN
Olha que beleza, já temos praticamente tudo para determinarmos as tensões máximas, só falta os esforços: