Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 141

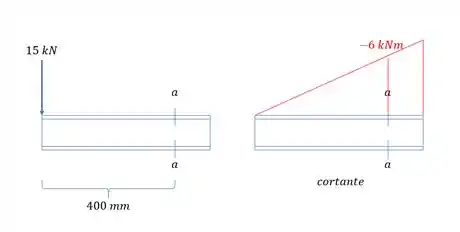
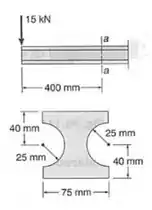
Par a viga abaixo com carregamento mostrado, e considerando a seção a - a , determinar:

  1. A maior tensão normal;
  2. A maior tensão de cisalhamento.

Passo 1

Fala ai pessoal, nosso objetivo aqui são dois, determinar a máxima tensão normal que age na nossa seção, e também a nossa máxima tensão cisalhante. Sabemos que nas vigas vamos ter que calcular as tensões pelas seguintes equações:

  • Tensão cisalhante devido o cortante

    • τ = V Q I b

    Em que:

    V = c o r t a n t e   a g i n d o   n a   s e ç ã o  

    Q = m o m e n t o   e s t á t i c o  

    I = m o m e n t o   d e   i n é r c i a  

    b = e s p e s s u r a   d a   r e g i ã o   q u e   d e s e j a   s e   s a b e r   a   t e n s ã o  

    Sabemos que a máxima tensão cisalhante vai ocorrer onde a LN passa, como a nossa seção é simétrica, sabemos que será bem no eixo de simetria, sendo assim, podemos definir o seguinte par aa tensão cisalhante:

    b = 25   m m

  • Tensão normal devido ao momento fletor

σ = - M y I

Em que:

M = M o m e n t o   f l e t o r   a g i n d o  

y = d i s t â n c i a   d a   L N   a t é   o   p o n t o   m a i s   d i s t a n t e   d e l a   n a   v e r t i c a l = 40   m m    

I = m o m e n t o   d e   i n é r c i a  

Sabendo as fórmulas, podemos seguir em frente, vamos nessa?

Passo 2

Vamos determinar primeiro o momento de inércia, já que temos que usar ele nas duas fórmulas. O nosso passo a passo é:

  • Primeiro determinamos uma divisão em seções mais simples (perceba que vamos usar uma retangular positiva e duas semicirculares negativas, com isso teremos que:

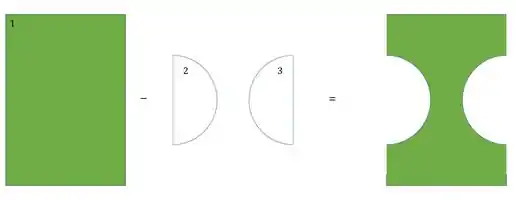
    • Como as 3 seções tem a mesma seção de simetria, não precisamos calcular novamente as áreas e distâncias até o centroide, baste recalcularmos os momentos de inércia, sendo assim teremos que:

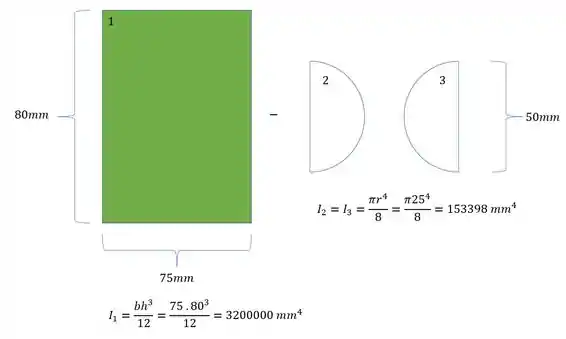
  • Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:

    • Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i

    Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:

    I = I 1 - I 2 + I 3

    I = 3200000 - ( 153398 + 153398 )

    I = 2893204   m m 4

    Passo 3

    Para o momento estático, da tensão cisalhante, precisamos determinar os seguintes dados:

  1. Ponto central onde passa a LN
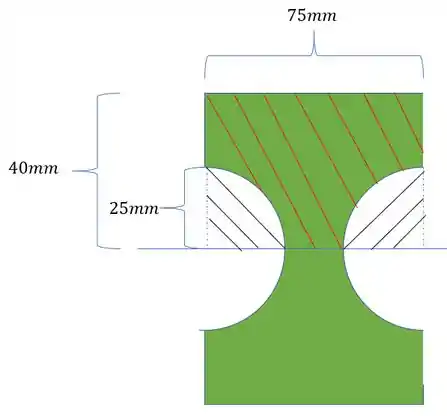
  • Área da região acima do ponto que se quer saber o cisalhamento

    • Perceba que queremos a área da região em verde, que tem o hachurado vermelho, e para isso, podemos considerar um retângulo com dimensões 75x40 e subtrairmos dele os ¼ de círculos com a hachura preta. Sendo assim, teremos que:

    A = 75 × 40 - 2 π 25 2 4 = 2018   m m 2

  • Distância do centroide da área até a LN

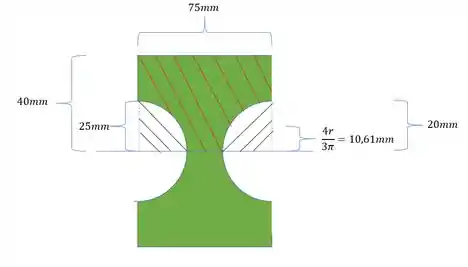
    • Perceba que seria muito difícil encontrar o centroide unicamente da parte verde, por isso, encontrei o centroide da parte retangular com 75 × 40 e da parte ¼ de círculo, ou seja, como o momento estático é a área multiplicada pela distancia do centroide até a LN, basta usarmos a mesma formula anterior, só que com as distancias atualizadas para cada uma das áreas (uma positiva e a outra negativa, com isso teremos que:

    Q = A 1 y 1 + A 2 y 2   = 75 × 40 × 20 - 2 π 25 2 4 × 10,61 = 49584   m m 3

    Olha que beleza, já temos praticamente tudo para determinarmos as tensões máximas, só falta os esforços:

    Passo 3

  • Esforço cortante

    • Como a nossa seção só possui uma carga constante e vertical, podemos desenhar o nosso diagrama de cortantes como sendo:

  • Esforço Momento fletor

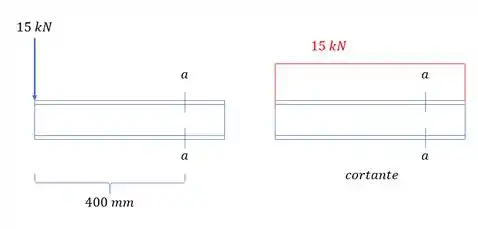
    • Como a nossa seção só possui uma carga constante e vertical, podemos desenhar o nosso diagrama de momentos como sendo:

  • Tensão Máxima cisalhante devido ao cortante:

    • V = 15 k N

    Q = 49584   m m 3

    I = 2893204   m m 4

    b = 25   m m

    τ = V Q I b = 15 k N .     49584   [ m m 3 ]     2893204   m m 4   .   25   [ m m ] = 0,0103   G P a = 10,3   M P a

  • Tensão Máxima normal devido a momento:

    • M = - 6   k N m = - 6000   k N m m

    y = 40   m m

    I = 2893204   m m 4

    σ = - M y I = - - 6000   k N m m . 40 m m 2893204   m m 4 = 0,08295   G P a = 82,95   M P a

    Resposta

    τ = 10,3   M P a

    σ = 82,95   M P a

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Determine a localização e do centro de cisalhamento (ponto O ) para o elemento de paredes finas com a seção transversal mostrada na figura, onde b 2b 1 . Os segmentos do elemento têm a mesma espessura
    Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
    Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
    Se a cantoneira tiver espessura de 3 m m , altura h = 100 m m e for submetida a um cisalhamento V = 50N , determine o fluxo de cisalhamento no ponto A e o fluxo de cisalhamento máximo na cantoneira.
    A cantoneira está sujeita a um cisalhamento V = 10k N . Faça um rascunho da distribuição do fluxo de cisalhamento ao longo da aba AB. Indique os valores numéricos em todos os picos. A espessura é 6m m