Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 10
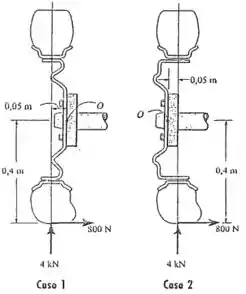
O cubo da roda pode ser conectado ao eixo com deslocamento negativo (esquerda) ou com deslocamento positivo (direita). Se o pneu está sujeito às cargas normal e radial conforme mostrado, determine o momento resultante dessas cargas em relação ao ponto no eixo para os dois casos.
Passo 1
Para determinar o momento gerado pela força é necessário determinar a distância do ponto até o ponto de atuação das forças0 onde os momentos serão aplicados. Assim, os eixos e serão considerados respectivamente a linha horizontal e a linha vertical.
Logo, para a componente horizontal da força, a distância até o braço do momento para ambos os casos será de:
E para a componente vertical da força será de:
Passo 2
Portanto, assumindo que o momento seja positivo no sentido anti-horário, tem-se que o momento para o caso 1 será de:
E o momento para o caso 2 será de:
Resposta
no sentido anti-horário.
no sentido anti-horário.