75. Se , determine o momento de binário resultante.

Vamos começar olhando para o par .

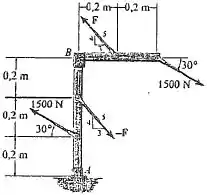
Nessa situação teremos que decompor nossas forças na vertical e na horizontal, para isso vamos usar o que a figura nos dá, que é aquele pequeno triangulo nos vetores das forças que indica uma proporcionalidade, então se quisermos a componente vertical da força, basta multiplicá-la por e se quisermos a horizontal, multiplicámos por .

Repara que para a força à direita de , a componente horizontal não gera momento em porque sua linha de ação passa por ele. O mesmo acontece com a componente vertical da força localizada abaixo de .

Então a componente vertical da força a direita de é

E a distância perpendicular entre e a linha de ação da força é

Como o momento que ela causa em é no sentido anti-horário, ele fica positivo

Já para a componente horizontal da força localizada abaixo de ,

Também no sentido anti-horário:

Acontece o mesmo para a força de . A força ao lado de só gera momento pela componente vertical, e a força abaixo só pela componente horizontal.

Aí o momento da força ao lado de fica:

Repara que fica negativo porque a força gera momento no sentido horário em relação a .

E o momento para força abaixo de

Também no sentido horário.

Usando como foi fornecido no enunciado, temos:

O sinal negativo indica que ele tem um sentido rotacional horário.