Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 84

84. Dois binários agem na mesma viga como ilustrado. Determine a intensidade de F de modo que o momento de binário resultante seja 300   N ⋅ m anti-horário. Onde atua na viga o binário resultante?

Passo 1

Fala!

A última pergunta já podemos responder de cara, como o momento de binário é um vetor livre ele causa o mesmo efeito independentemente de onde ele é aplicado no corpo, logo ele pode ser determinado em relação a qualquer ponto do corpo, logo esse momento pode atuar em qualquer parte da viga.

Então o enunciado também quer é achar um F que produza um momento binário que junto com o momento binário de 2000   N seja igual a 300   N ⋅ m no anti-horário. Se a gente adotar esse sentido como positivo:

M R = 300   N . m

Vamos calcular o momento binário usando a análise escalar:

M = F ⋅ d

Onde F é a intensidade das forças e d é a distância perpendicular ou braço de momento entre as forças.

Nessa situação teremos que decompor nossas forças na vertical e na horizontal para achar d para cada uma das componentes, porque nessa orientação é mais complicado de achar.

O momento binário resultante é a soma dos momentos binários das forças. Então a gente vai calcular os binários, somar e igualar a M R .

Bora!

Passo 2

Vamos começar calculando o momento binário da força F .   Para achar as componentes dela a gente vai usar o triângulo retângulo pequeno que aparece na figura do enunciado. O lado 3 é paralelo ao eixo y e o lado 4 paralelo ao eixo x .

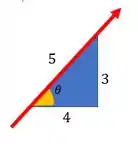
Usando trigonometria, a gente pode escrever que

F x = F cos ⁡ θ = F 4 5

F y = F   s e n   θ = F 3 5

d para a F x vai ser a distância x entre os pontos de aplicação da força:

d x = 0,4   m

E para F y , a distância em y :

d y = 0 , 15   m

Os momentos causados pelo par F x   e pelo par F y   estão no sentido anti-horário, então ambos são positivos:

M = d F

M 1 = F x d x = 4 5 F ⋅ 0,4

M 2 = F y d y = 3 5 F ⋅ 0,15

Passo 3

Agora vamos calcular o momento em relação ao par de 2 000 N . A distância entre a linha de ação dessas forças é:

d 3 = 0 , 15   m

E a orientação do momento é no sentido horário então esse vai ser negativo:

M 2 = - 0 , 15 ⋅ 2 000

Passo 4

Para calcular o resultante a soma a galera toda:

M R = M 1 + M 2 + M 2

Lembrando que M R = 300   N . m :

300 = F 4 5 0,15 + F 3 5 0,4 - 2000 ⋅ ( 0,15 )

⇒ 300 = 0,12 F + 0,24 F - 300

⇒ 300 = 0,36 F - 300

⇒ 0,36 F = 300 + 300

⇒ 0,36 F = 600

⇒ F = 1666,7

Resposta

A força deve ter intensidade de:

F = 1666,7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua o sistema de forças que age sobre o poste por uma força e momento de binário resultante no ponto A .
Substitua o sistema de forças que age sobre o poste por uma força e momento de binário resultante no ponto O .
Substitua as duas forças por uma força e momento de binário equivalente no ponto O . Considere F = 75N .
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro A B medida a partir de A .
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de A .