Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 62
Uma cunha de 8° é forçada sob a base B de uma máquina. Sabendo que o coeficiente de atrito estático entre todas as superfícies é 0,15, determine a força P necessária para mover a cunha, indique se a base da máquina deslizará no chão.
Passo 1
Vamos começar esse excercício desenhando o diagrama de corpo livre para a máquina:
Agora vamos aplicar o somatório de momento com relação ao ponto B:
Agora, aplicando o somatório de forças na direção :
Passo 2
Agora vamos analisar o diagrama de corpo livre para a cunha:
Como vimos na seção anterior do livro, o coeficiente de atrito pode ser escrito como:
Então, substituindo o valor do coeficiente de atrito dado no enunciado, temos:
Passo 3
Agora vamos desenhar o triângulo de forças para a cunha do passo 2:
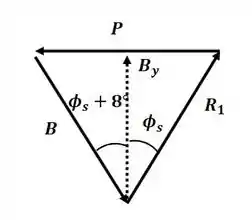
Agora podemos então calcular o valor máximo da força P (caso em que a máquina não se move):
Agora devemos verificar se a máquina irá ou não se mover, então, para isso, devemos calcular a força de atrito máxima nos pontos A e B, que será dada por:
Então, como , a máquina se moveria junto com a cunha, então, na verdade ficará limitado :
E, para esse valor, a base da máquina irá se mover.