Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 65

Resolva o Problema 8.64 considerando que os rolos são removidos e o μ s é o coeficiente de atrito entre todas as superfícies de contato.

Passo 1

Vamos começar esse excercício desenhando o diagrama de corpo livre para a cunha:

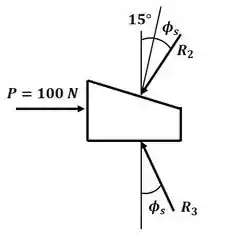
Passo 2

Agora vamos desenhar o triângulo de forças para o sistema do passo 1:

Aplicando a lei dos senos para esse triângulo, temos:

R 2 s e n ( 90 ° - ϕ s ) = P s e n ( 15 ° + 2 ϕ s ) → R 2 = s e n ( 90 ° - ϕ s ) P s e n ( 15 ° + 2 ϕ s )

Essa será nossa equação 1.

Passo 3

Agora vamos analisar o diagrama de corpo livre do bloco:

Com base nesse DCL, vamos desenhar o triângulo de forças:

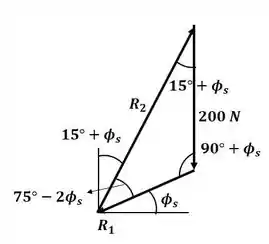
Aplicando a lei dos senos para esse triângulo, temos:

R 2 s e n ( 90 ° + ϕ s ) = W s e n ( 75 ° - 2 ϕ s ) → R 2 = s e n ( 90 ° + ϕ s ) W s e n ( 75 ° - 2 ϕ s )

Agora vamos igualar essa expressão à equação 1 obtida no passo 2:

s e n 90 ° - ϕ s P s e n 15 ° + 2 ϕ s = s e n ( 90 ° + ϕ s ) W s e n ( 75 ° - 2 ϕ s )

Substituindo os valores conhecidos de P e W :

s e n 90 ° - ϕ s 100 s e n 15 ° + 2 ϕ s = s e n ( 90 ° + ϕ s ) 200 s e n ( 75 ° - 2 ϕ s )

Agora, resolvendo por tentativa e erro, ou colocando essa expressão em uma calculadora, o resultado será:

ϕ s = 5,78 °

E, conforme vimos na seção anterior, podemos calcular o coeficiente de atrito através de:

μ s = tg ⁡ ϕ s = tg ⁡ 5,78 ° → μ s = 0,101

Resposta

μ s = 0,101

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
Na morsa de bancada mostrada, o mordente móvel D está rigidamente ligado a lingueta A B que se encaixa com folga no corpo fixo da morsa. O parafuso de rosca simples é rosqueado na base fixa e tem um d
Considerando no Problema 8.70 que uma rosca à direita seja usada em ambas as barras A e B , determine a intensidade do torque que deve ser aplicado à luva a fim de girá-la.
No problema 8.72 , a força de aperto de 4,5N foi obtida apertando-se a morsa. Determine o torque que deve ser aplicado ao parafuso para afrouxar a morsa.
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque