Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 64

O bloco de 200 N repousa sobre uma cunha de peso desprezível, como mostra a figura. O coeficiente de atrito estático é o mesmo entre as superfícies da cunha, e o atrito entre o bloco e a parede vertical pode ser desprezado. Para , determine o valor de para que o movimento seja iminente. (Dica: Resolva a equação por tentativa e erro).

Passo 1

Vamos começar esse excercício desenhando o diagrama de corpo livre para a cunha:

Passo 2

Agora vamos desenhar o triângulo de forças para o sistema do passo 1:

Precisamos descobrir o valor da componente , para isso, vamos analisar o diagrama de corpo livre do bloco:

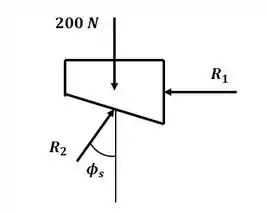
Aplicando o somatório de forças na direção :

Passo 3

Então, olhando novamente para o triângulo de forças da cunha, podemos escrever:

Substituindo os valores conhecidos:

E, conforme dito no enunciado, resolvendo por tentativa e erro, chegamos no resultado:

E, conforme vimos na seção anterior, podemos calcular o coeficiente de atrito através de:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição do macaco de automóvel mostrado na figura é controlada por um parafuso A B C com rosca simples em cada extremidade (rosca à direita em A , rosca à esquerda em C ). Cada rosca tem um passo de

Uma cunha A de peso desprezível é forçada entre dois blocos B e C de 450N que repousam em uma superfície horizontal. Sabendo que o coeficiente de atrito estático em todas as superfícies de contato é 0

A parte da máquina A B C é sustentada por uma dobradiça sem atrito em B e uma cunha de 10 ° em C . Sabendo que o coeficiente de atrito estático nas superfícies da cunha é 0,20 , deteremine ( a ) a for

No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque

No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque