Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 3
Dados os três vetores não nulos , e , mostre que se , os três vetores necessitam estar no mesmo plano.
Passo 1
Para representar os vetores, pode-se fazer um desenho tal que:
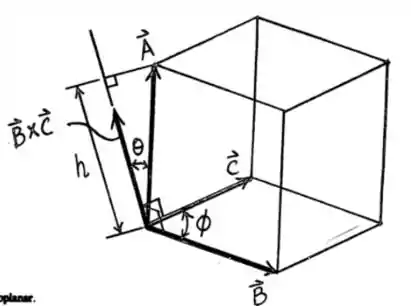
Passo 2
Assim, para determinar a intensidade do produto triplo escalar deve-se aplicar o módulo no mesmo. Com isso, tem-se que:
Passo 3
Pelo desenho, podemos observar um valor que pode ser substituído na última equação:
Como representa o valor absoluto do produto vetorial, ele pode ser substituído pelo seu equivalente, ou seja:
Essa equação representa o volume do paralelepípedo.
Dessa forma, caso , o volume do paralelepípedo é nulo, o que significa que os vetores , e são coplanares.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
3.11. Sabe-se que é necessária uma força com um momento de 960N ⋅ m em relação a D para endireitar o mourão CD. Se a capacidade do guincho AB 2400N , determine o valor mínimo da distância d para se cr
A cancela de travessia da linha férrea consiste em um braço de 100 kg com um centro de massa em Ga e o contrapeso de 250 kg com um centro de massa em GW. Determine a intensidade e o sentido direcional
Determine o momento produzido por cada força em relação ao ponto B.
O torquímetro ABC é usado para medir o momento ou torque aplicado a um parafuso quando ele está localizado em A e uma força é aplicada à alça em C. O mecânico lê o torque na escala em B. Se uma extens
A força de 70 N age na extremidade do tubo em B. Determine (a) o momento dessa força em relação ao ponto A e (b) a intensidade e a direção de uma força horizontal, aplicada em C, que produz o mesmo mo