Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 4
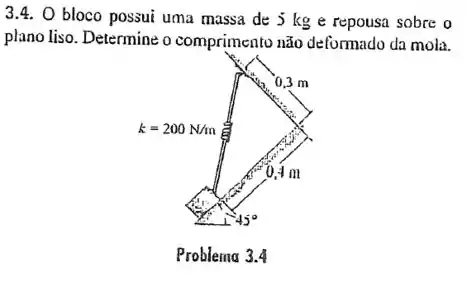
Passo 1
Antes de qualquer exercício de estática devemos desenhar o diagrama de corpo livre.
Nessa caso vamos analiser o bloco:
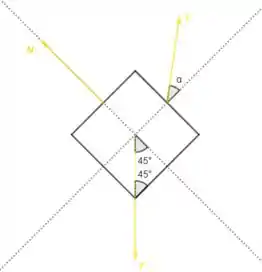
A força normal sempre atua perpendicularente a algum plano, nesse caso o plano liso inclinado.
A força Peso sempre irá atuar para baixo.
E a força está atuando sobre o bloco com um ângulo de , que pode ser descoberto usando relações trigonométricas.
Passo 2
Como o bloco não se meche, a soma de forças em e em deve ser zero.
A soma das forças em são:
Vamos calcular :
Continuando a equação:
O peso é igual a massa vezes a gravidade:
Passo 3
Já descobrimos a força que é a força que a mola faz sobre o bloco, então não precisamos montar as equações para o eixo .
Agora vamos analisar essa força. Qulquer força elástica é da forma:
Nesse caso, como o enunciado nos diz o valor da constante elástica da mola, vamos ter que
Então a deformação da mola vale:
Por pitagoras conseguimos descobrir o tamanho do cabo com a mola, que vou chamar de :
Esse é o comprimento da mola esticada, o comprimento não deformado, , vai ser: