Exercícios de Momentos em Duas Dimensões - Lista de Exercícios Resolvida
Questão 1
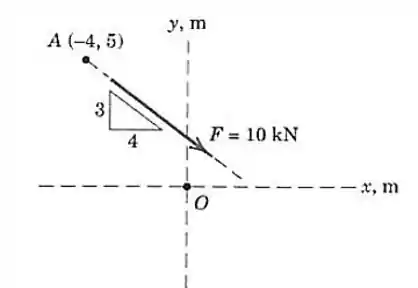
A força de é aplicada no ponto . Calcule o momento de em relação ao ponto . Determine os pontos nos eixos e em relação aos quais o momento de vale zero.
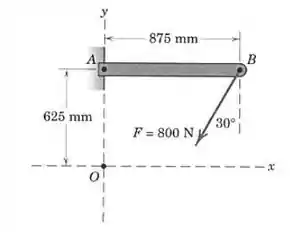
Questão 2
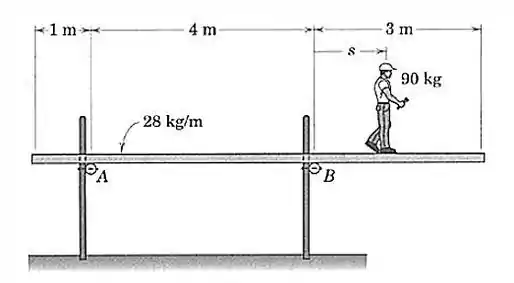
A plataforma uniforme, que tem uma massa por unidade de comprimento de , está simplesmente apoiada sobre barras de apoio em e em . Um trabalhador de construção civil com sai do ponto e anda para a direita. Em que posição o momento combinado do peso do homem e da plataforma será zero em relação ao ponto ?
Questão 3
Um mecânico puxa a chave de boca de com a força de mostrada. Determine o momento da força em relação ao centro do parafuso.
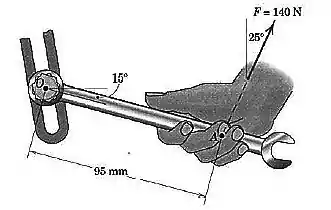
Questão 4
A força de módulo é aplicada à roda dentada. Determine o momento de em relação ao ponto .
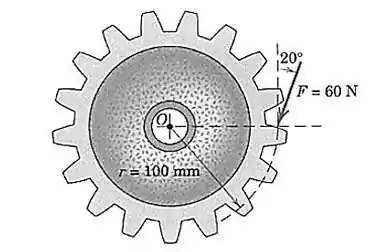
Questão 5
Determine o momento da força de :
- Em relação ao ponto usando o teorema de Varignon.
- Em relação ao ponto por um enfoque vetorial.
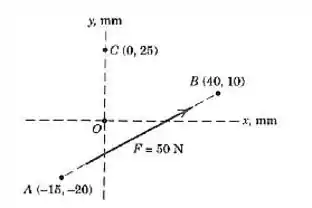
Questão 6
O componente de controle do acelerador pivota livremente em Se uma mola de torção interna exerce um momento de retorno sobre o componente, quando ele está na posição mostrada, determine, para a finalidade de projeto, a força trativa necessária no cabo do acelerador para que o momento resultante em torno de seja zero. Observe que quando é zero, o componente se apóia no parafuso do ajuste da marcha lenta em
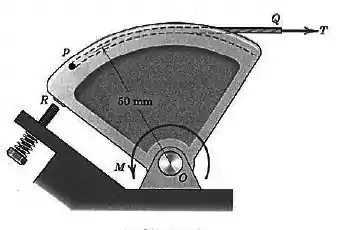
Questão 7
A força de é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto
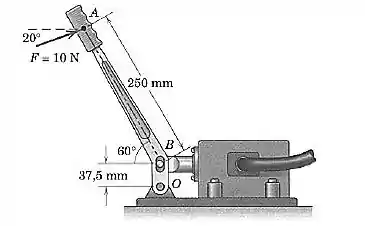
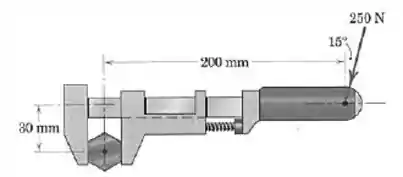
Questão 8
Calcule o momento da força de na manopla da chave inglesa em relação ao centro do parafuso.
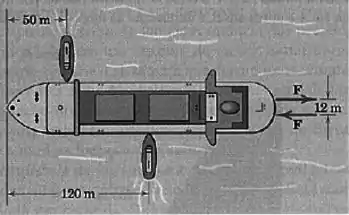
Questão 9
Cada hélice de um navio de duas hélices desenvolve um empuxo de na velocidade máxima. Ao manobrar o navio, uma hélice está girando a toda velocidade para frente e a outra a toda velocidade no sentido reverso. Que empuxo cada rebocador deve exercer no navio para contrabalancear o efeito das hélices?