Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 11
3.11. Sabe-se que é necessária uma força com um momento de em relação a D para endireitar o mourão CD. Se a capacidade do guincho AB , determine o valor mínimo da distância d para se criar o momento especificado em relação ao ponto D.
Passo 1
Bem, quase todo exercício de mecânica fica mais simples resolver se fizermos um desenho da situação destacando o que a gente precisa.
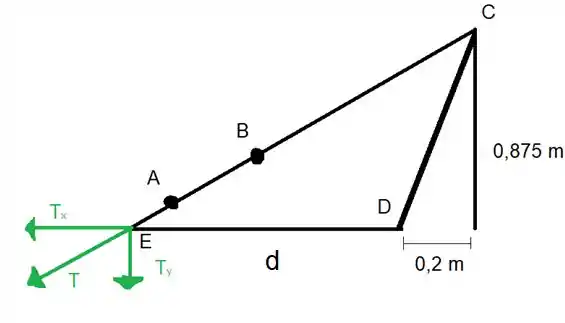
Esse é a tração que o guincho exerce no ponto C, já está decomposto nos eixos, mas temos que achar seus valores, para isso vamos usar o grande triângulo que a imagem forma
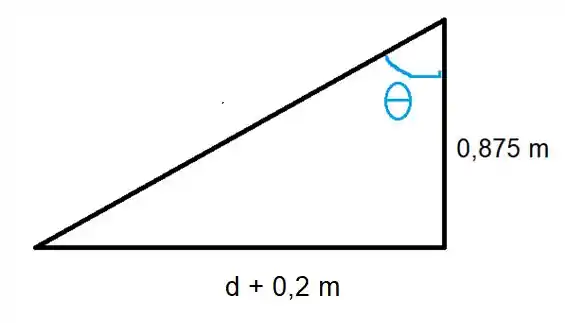
Vamos achar o valor da hipotenusa por Pitágoras:
Agora a gente pode obter os valores de e
E agora
Passo 2
O momento de uma força é definido por
Onde
Momento
Força
distância
Como temos a força decomposta, vamos usar
Vamos começar por
Agora
Então
Passo 3
O enunciado nos diz que o momento tem que ser de , então
Então temos que isolar
Vamos elevar os dois lados ao quadrado para sumir com a raiz
Então
E chegou a hora da famosa equação de Bhaskaras
Só vamos ter um valor possível para , o valor em que ele é positivo