Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 51
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado. Determinar também o máximo valor absoluto fletor na viga.
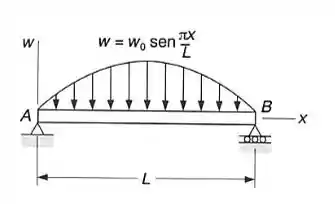
Passo 1
E ai gurizada tudo beleza? Espero que sim!!
Para resolvermos este exercício vamos levar em consideração a seguinte analogia..
Consideramosssss que se:
M= 0 em x=0
M=0 em x= L
Então teremos a seguinte situação pessoal
Se (dividimos a distância ao meio considerando a centroide, lembre-se que a carga distribuída, consideramos ela para fins de cálculo em uma carga pontual)
substituindo x= L/2 temos.............
Gurizada como
Resposta
Exercícios de Livros Relacionados
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo momento fl
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.
(a) Usando funções de singularidade, determine a intensidade e a localização do momento fletor máximo para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo moment
Uma viga está sendo projetada para ser vinculada e carregada conforme mostra a figura. (a) Usando funções de singularidade, encontre a intensidade e a localização do momento fletor máximo na viga. (b)
(a) Usando funções de singularidade, determine a intensidade e a localização do momento fletor máximo para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo moment