Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 41

Resolver o Prob.5.40, considerando que a altura da placa é aumentada de 400   m m para 600 m m .

Passo 1

Queremos determinar a máxima força que age em cada um dos parafusos, sabemos que a carga por metro é determinada da seguinte maneira

q = V Q I

E como queremos a força que age em cada parafuso, precisamos multiplicar a carga por metro pela distância entre parafusos, sendo assim teremos que:

F = q s

Sendo “s” a distância entre parafusos também sabemos que:

V = c o r t a n t e   a g i n d o   n a   s e ç ã o  

Q = m o m e n t o   e s t á t i c o  

I = m o m e n t o   d e   i n é r c i a  

s = 120   m m

Agora precisamos determinar o momento estático e o momento de inércia, para isso temos um passo a passo.

Passo 2

Vamos determinar primeiro o momento de inércia, para isso precisamos determinar algumas coisas, para isso temos que fazer o seguinte passo a passo.

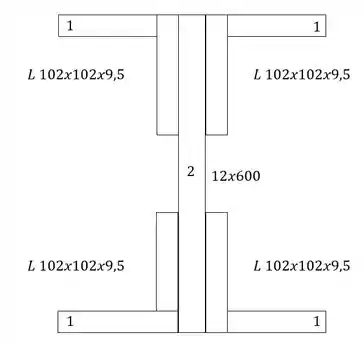
  • Primeiro determinamos uma divisão em seções mais simples

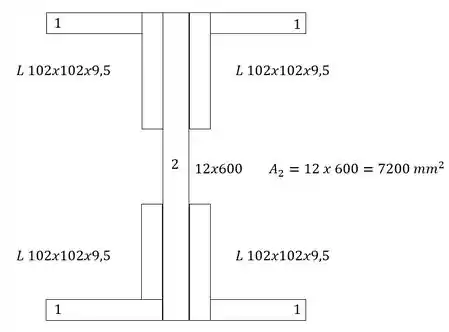
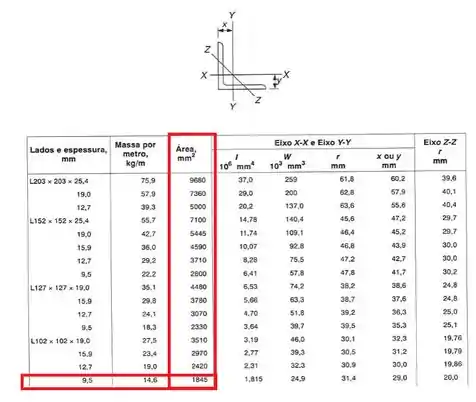
  • Em segundo determinamos as áreas da nossa seção

    • A 1 = 1845   m m 2

  • Em terceiro determinamos a distância dos centroides dos elementos até a LN, e como a seção é simétrica, está no centro da seção total, sendo assim teremos que:

  • Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:

    • I 1 = 1,815   .   10 6   m m 4

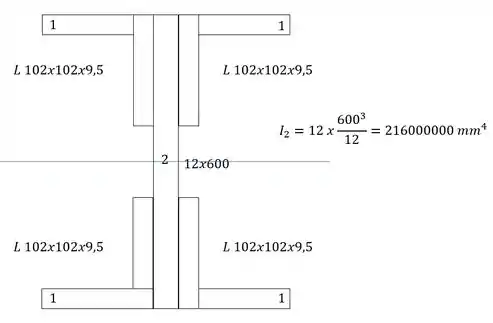
    Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i + A i d i 2

    Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:

    I = I 2 + 4 I 1 + A 1 d 1 2

    I = 216000000 + 4 1,815   .   10 6 + 1845   .     2 71 2

    I = 765254580   m m 4

    Passo 3

    Para o momento estático, iremos considerar apenas uma das cantoneiras trabalhando, ou seja, ela irá super solicitar o parafuso, causando assim a máxima tensão cisalhante nele, então só precisamos de duas coisas, área da cantoneira e distância do centroide dela para a LN

    Q = A 1 y 1   = 1845   .     2 71 = 499995   m m 3

  • Assim podemos determinar a máxima carga por metro que podemos ter:

Sabemos que:

V = 240   k N = 240000   N

Q = 499995   m m 3

I = 765254580   m m 4

q = V Q I = 240000     .   499995     765254580 = 156,81 N m m

Multiplicando isso pela distancia entre os parafusos teremos que:

F = q S = 156,81   .   120 = 18817,2   N  

Se já temos a força que age no parafuso, para termos a tensão nele, basta dividirmos pela área dele, como ele tem um diâmetro de 22 m m , basta fazermos o seguinte:

τ p a r a f u s o = F A = 18817,2 π D 2 4 = 4   .   18817,2 π D 2 = 4   .   18817,2 π 22 2 = 49,5   M P a

Resposta

τ p a r a f u s o = 49,5   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

147. Para a viga caixão do problema 5.146 , determinar (a) a maior força cortante horizontal permissível na viga; (b) a correspondente tensão de cisalhamento máximo na viga
148. Duas forças são aplicadas a um tubo A B , como mostrado. Sabendo-se que o tubo tem diâmetros, interno e externo, iguais a 35m m e 42m m , respectivamente, determinar as tensões, normal e de cisal
149. Resolver o problema 5.148 , considerando que a força de 1500N é dirigida para cima
As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado de tensões mostrado determinar: (a) a tensão de cisalhamento no plano, em um plano paralelo as fibras;(b) a
Duas peças de madeira de 80x120mm, de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na jun