Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 80a
Determinar a reação no apoio móvel e desenhar o diagrama de momento fletor para a viga com o carregamento mostrado.
Obs: determinação dos valores da viga no estado isostático para o caso 1
Passo 1
Então meu povo, vamos de mais um exercício? Pode parecer um exercício um pouco complexo por ser hiperestático, mas não tema, nada que não possamos resolver bem tranquilo, então me segue que é sucesso.
Apesar de estarmos em um estado hiperestático, podemos forçar a nossa barra a virar um somatório de estados isostáticos. No caso, o que vou fazer é quebrar um vínculo de momento no apoio A, e assim vamos ter a seguinte divisão de cargas na nova viga: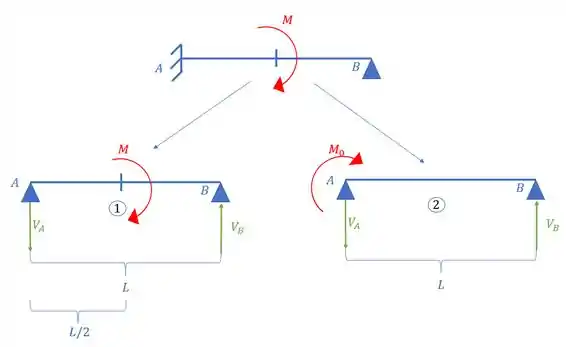 
Agora lembre-se do seguinte, sabemos que na verdade em A temos um engaste, certo? Logo sabemos que obrigatoriamente o ângulo lá é zero. Porém podemos ver que nas vigas isostáticas 1 e 2 teremos ângulos formados diferentes de zero em A, o que isso significa? Que se somarmos o ângulo que temos na viga 1 com o que temos na viga 2, temos que ter zero como somatório deles, e daí conseguimos tirar o nosso , e a partir deles podemos determinar a nossa reação no apoio móvel, beleza? Então vamos lá.
Passo 2
Vale lembrar que dividimos o problema em duas partes, nessa primeira parte determinamos as duas vigas e o ângulo da viga 1, e na parte 2, ou b, vamos determinar o ângulo da viga 2, e a reação de apoio que precisamos, beleza? Então vamos lá. Como a nossa viga 1 é isostática, podemos determinar as suas reações de apoio.
Agora perceba o seguinte, suponha que ao invés de termos os apoios em A e B, vamos supor que eles são cargas aplicadas na nossa viga, e que no caso no ponto A temos um engaste, então basta desenharmos o diagrama de cada carga com relação ao ponto A, assim, teremos que:
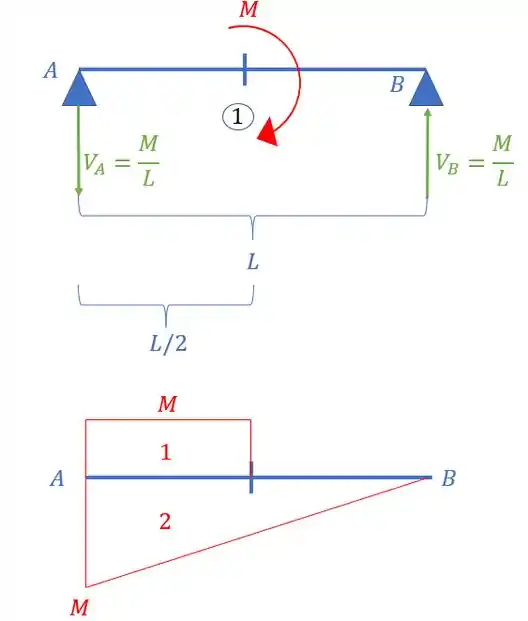
E sabemos que devemos dividir o nosso diagrama por referente a cada uma das barras, e assim teremos que:
Passo 3
Agora, pensa no seguinte, como eu disse, quando tínhamos cargas simétricas, poderíamos considerar um ponto em que sabíamos que a deflexão era zero, porém, agora não sabemos mais onde temos essa deflexão, vamos partir direto para o que sabemos, que nesse caso é a deformação, e como a deformação vai nos ajudar a determinar a declividade? Muito simples, podemos determinar a deformação de B com relação a A da seguinte maneira:
E pensa no seguinte, queremos saber quanto vale o ângulo em A, certo? Vamos isolar o ângulo:
E se multiplicarmos tudo por L, obtemos exatamente as deformações, mas perceba que a do ângulo A eu não irei modificar.
E sabemos que a deformação em B é zero, assim temos que:
E para determinarmos a deformação precisamos de todas as áreas entre A e B e das distâncias desses centroides ATÉ B, bem importante lembrar que sempre determinamos a distância com relação ao primeiro termo do subscrito . Dividindo o nosso diagrama em áreas mais simples temos que:
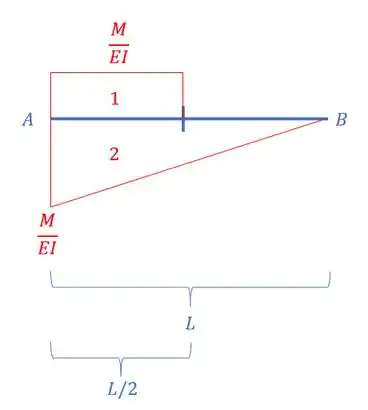
E além das áreas precisamos da distância de cada centroide até o nosso ponto B, assim teremos que:
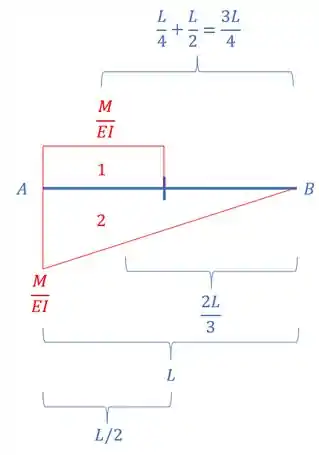
Assim podemos definir que:
Mas lembre-se que o objetivo é o ângulo, com isso teremos que: