Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 02

Determinar:

  1. O torque T que causará uma tensão de cisalhamento máxima de 45   M p a no cilindro vazado de aço, como indicado;
  2. A máxima tensão de cisalhamento causada pelo mesmo torque T, em um eixo cilíndrico maciço de mesma área e seção transversal.

Passo 1

O enunciado nós da os seguintes dados:

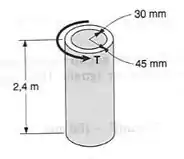
O enunciado diz que a tensão máxima suportada pelo tubo é de 45   M P a , sendo assim usaremos a seguinte equação:

τ = T ρ J

Sabemos que a máxima tensão, usa o maior raio, sendo assim teremos que:

r m a x = r e = 45   m m

Calculando o polar de inércia teremos que:

J = π ( r e 4 - r i 4 ) 2 = π ( 45 4 - 30 4 ) 2 = 5168902   m m 4

E no item A) queremos saber o máximo torque que podemos usar, sendo assim teremos que:

τ = 45   M P a = 45 N m m 2

Substituindo teremos que:

45 = T   .   45 5168902

T = 5168902   N m m = 5,2   k M m

Passo 2

No item B) queremos manter a mesma área da barra furada, porém com uma barra de eixo maciço, sendo assim teremos que o raio da nova barra será:

A = π 45 2 - 30 2 = 3534,3   m m 2

Agora se quisermos ter o raio da barra maciça teremos que:

A = π r 2 = 3534,3   m m 2  

r = 33,541

Calculando o máximo cisalhante teremos que:

τ = T r J

E sabemos que:

J = π r 4 2

Substituindo teremos que:

τ = T r π r 4 2

τ = 2 T π r 3 = 2   .   5,2   .   1000 π   .     33,541 3 = 0,08773   G P a = 87,73   M P a

Resposta

  1. T = 5,2   k M m
  2. τ = 87,73   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento vazado com seção transversal mostrada é formado a partir de uma lâmina de metal com espessura de 2 mm. Sabendo que a tensão de cisalhamento no pode exceder 3 MPa, determine o maior torque
Um elemento vazado com seção transversal mostrada é formado a partir de uma lâmina de metal com espessura de 2 mm. Sabendo que a tensão de cisalhamento no pode exceder 3 MPa, determine o maior torque
Um torque de 90 N*m é aplicado a um eixo vazado com a seção transversal mostrada na figura. Desprezando o efeito das concentrações de tensão, determine a tensão de cisalhamento aos pontos a e b.
Uma barra vazada com a seção transversal mostrada na figura deve ser formada a partir de uma chapa metálica de 1,524 mm de espessura. Sabendo que um torque de 141,2 N m será aplicado a barra, determin
Um eixo cilíndrico vazado foi projetado para ter uma espessura uniforme de 0,1 in. Defeitos de fabricação, no entanto, resultam em eixos com a seção transversal mostrada. Sabendo que um torque de 15k