Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 125

Uma barra de latão tem a seção vazada mostrada na figura. Sabendoque a tensão de cisalhamento não pode 84 MPa e desprezando o efeito da concentração de tensões, determine o maior torque possível de ser aplicado ao eixo

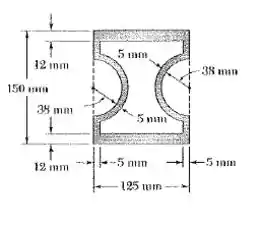
Passo 1

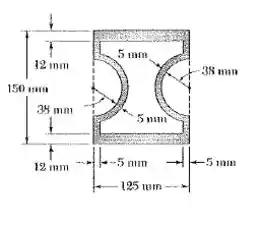
Dessa questão temos que

τ a d m = 84   M P a

A área contornada pela linha centra vai ser a parte chatinha dessa questão. Ela pode nos ser dada por

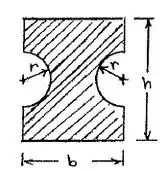
Se você for perceber é simplesmente m retângulo com duas semi-circonferencias subtraídas.

b = 125 - 5 = 120 m m

h = 150 - 12 = 138   m m

r = 38 - 2,5 = 35,5   m m

A = b h - 2 × π r 2 2 = 120 138 - π 35,5 2 = 12600 m m 2 = 1 2 , 6 × 10 - 3   m 2

Passo 2

Lembrando que τ a d m = 84   M P a

τ a d m = T 2 A t m i n  

Onde o t m i n = 0,005   m

T = 2 A t m i n τ a d m = 2 12,6 × 10 - 3 0,005 84 × 10 6 = 10584   N . m = 10,58   k N . m

Resposta

T = 10,58   k N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de aço com 2438 mm de comprimento e seção transversal W 200 × 46,1 está submetida a um toriqe de 565 N.m. As propriedades da seção laminada são dadas no apêndice C. Sabendo que G = 77,2 GPa,
Um torque T de5 kN.m é aplicado a um eixo de seção vazada com a seção transversal mostrada na figura. Desprezando o efeito das concentrações de tensão, determine a tensão de cisalhamento nos pontos a
Um torque de 90 N.m é aplicado a um eixo vazado com seção transversal mostrada na figura. Desprezando o efeito das concentrações de tensão, determine a tensão de cisalhamento nos pontos a e b.
Um eixo maciço de aço ( G = 77G P a ) de 30m m de diâmetro, gira com uma frequência de 30H z . Determinar a máxima potência que o eixo pode transmitir, sabendo-se que a tensão de cisalhamento admissív