Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 03
Um torque de é aplicado ao cilindro maciço mostrado. Determinar:
- A máxima tensão de cisalhamento;
- O percentual do torque absorvido pelo núcleo de diâmetro .
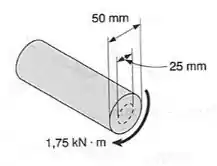
Passo 1
O enunciado nos dá os seguintes dados:
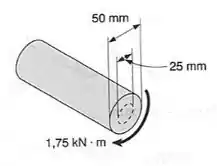
E a primeira pergunta é exatamente a tensão cisalhante máxima, e já sabemos que a nossa fórmula é:
Como queremos o máximo, vamos usar o raio máximo que vai ser dado por:
E no momento polar de inércia teremos que:
Substituindo teremos que:
E sabemos que:
Substituindo sabemos que:
Passo 2
No item B queremos saber o quanto o centro com diâmetro de 25mm absorvem de momento. Sabemos que a tensão cisalhante cresce linearmente, sendo assim teremos que:
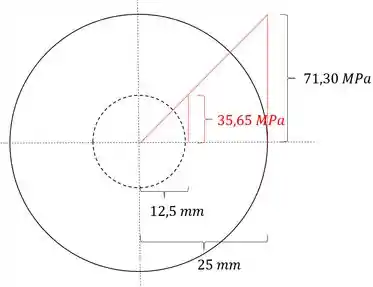
usando o raio de 12,5 mm, podemos determinar o quanto de torção foi absorvido por esse ponto, sendo assim teremos que:
E sabemos que:
Substituindo teremos que:
Como queremos a porcentagem devemos fazer o seguinte:
Resposta
Exercícios de Livros Relacionados
Determine:O torque que pode ser aplicado a um eixo maciço de 75m m de diâmetro sem que seja excedida a tensão admissível de cisalhamento de 83M p a ;Idem ao item a), considerando que o eixo maciço dev
Os torques são exercidos nas polias A, B e C. Sabendo-se que ambos os eixos são maciços, determinar a máxima tensão de cisalhamento:No eixo AB;No eixo BC.
Sob condições normais de operação, um motor elétrico exerce um torque de 1350N m , em E . Sabendo-se que todo o eixo é maciço, determinar a máxima tensão de cisalhamento:No eixo BC;No eixo CD;No eixo
Resolver o P r o b .3.6 , considerando que um furo de diâmetro igual a 25,4 m m foi broqueado ao longo de todo o eixo.
Os torques mostrados são aplicados às polias A, B, C e D. Sabendo-se que todo o eixo é maciço, determine:Em qual trecho do eixo ocorre a maior tensão de cisalhamento;A intensidade dessa tensão.