Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 47
Determine as coordenadas do centroide da área trapezoidal mostrada.
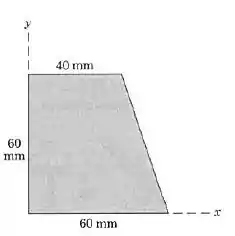
Passo 1
Sabendo que aa equação para encontrar o centro de massa é dado por:
Dessa maneira, vamos primeiro encontrar os centros de cada parte.
Passo 2
Mas antes vamos separar cada componente, de tal modo que:
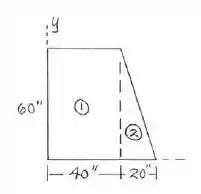
Pronto! Escolhido os componentes vamos montar uma tabela com cada parte
Passo 3
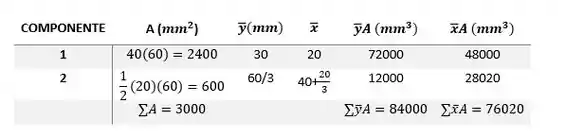
No primeiro componente, vemos que a área é o comprimento 40mm vezes a altura 60mm. Com isso, tanto o quando o fica no meio desses valores.
Já no segundo componente, que é um triangulo, temos que a área é metade do seu comprimento vezes a altura. E sabendo que o centroide de um triângulo é dado por:
Cuidado! Ao calcular lembre-se de somar mais 40 pois é em relação a origem que delimitamos.
Passo 4
Agora só basta substituir na equação que teremos nosso ponto: