Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 134
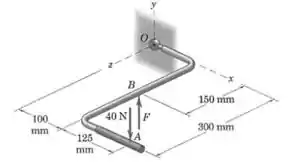
Para reduzir o momento indesejável em relação ao eixo , um mecânico usa sua mão esquerda para sustentar o cabo da chave no ponto . Que força direcionada para cima, , deve ser exercida para que não haja momento em relação ao eixo ? Qual é, então, o momento resultante em relação a ?
Passo 1
Vamos pensar na definição de momento de uma força:
Primeiro precisamos calcular o momento gerado pela força de . O vetor posição que liga o ponto e o ponto onde a força é aplicada pode ser escrito da seguinte forma:
E agora é interessante reescrever a equação do momento da seguinte forma:
E podemos usar a propriedade distributiva do produto vetorial:
Passo 2
E a nossa ideia é que a força anule perfeitamente o momento em torno do eixo , e portanto ela precisa ser simétrica à componente do momento que acabamos de calcular:
Aquele índice no parênteses está ali para lembrar de que essa igualdade se refere apenas à componente do momento.
E o vetor posição da força (veja o desenho) pode ser escrito da seguinte forma:
E o vetor da força é:
Beleza, então a componente na direção do eixo é :
Passo 3
Ok, já respondemos a primeira pergunta. E agora que sabemos o módulo da força podemos calcular o momento total em relação a :
Agora é só somar os dois momentos:
Resposta
O módulo da força deve ser , e o momento total em relação ao ponto será .