Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 92

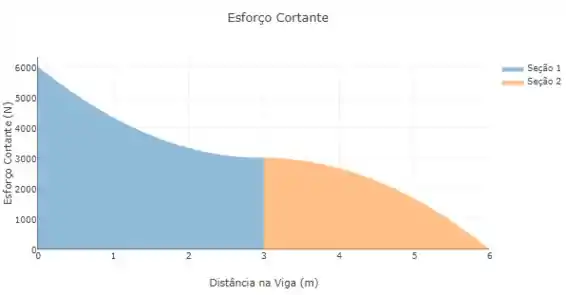
Determine os diagramas de força cortante e de momento fletor para a viga.

Passo 1

Oi, tudo bem? Vamos analisar esta questão.

O exercício nos pede para determinar os diagramas de força cortante e de momento fletor para a viga em questão. Vamos aprender a construir estes diagramas.

A primeira coisa a se fazer é o diagrama de corpo livre da viga com as reações de apoio:

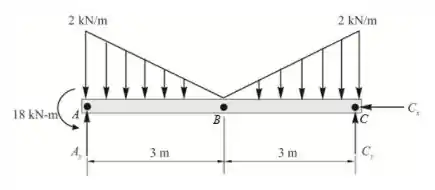
Agora vamos descobrir o valor destas reações.

Se fizermos o somatório de momento em A , teremos que:

∑ M A = 0

C y 6 + 18 - 1 2 2 3 1 3 ⋅ 3 - 1 2 2 3 3 + 2 3 ⋅ 3 = 0

C y = 0

A partir do somatório de forças na vertical, temos que:

∑ F y = 0

A y + C y - 1 2 2 3 - 1 2 2 3 = 0

A y = 6   k N

Para a força externa agindo na horizontal, temos que:

∑ F x = 0

C x = 0

Passo 2

Agora que temos o valor das reações. Vamos calcular a força cortante e o momento fletor nas seções de interesse.

Para o ponto A , temos que:

V A = A y

V A = 6   k N

No ponto B , temos que:

V B = - 1 2 2 3 + V A

V B = - 3 + 6

V B = 3   k N

Para o ponto C , temos que:

V C = - 1 2 2 3 + V B

V C = - 3 + 3

V C = 0

Passo 3

Analisando o momento fletor, temos que:

M A = - 18   k N ⋅ m

No ponto B , temos:

M B = M A + 1 2 2 6 2 3 ⋅ 3

M B = - 18 + 1 2 2 6 2 3 ⋅ 3

M B = - 6   k N ⋅ m

E no ponto C , temos que:

M C = - M A - A y 6 + 1 2 2 6 2 3 ⋅ 3 + 3 + 1 2 2 6 1 3 ⋅ 3

M C = - 6 A y + 36

M C = - 6 6 + 36

M C = 0

Passo 4

Agora é só construir os diagramas com os valores em cada ponto.

Os diagramas de força cortante e momento fletor ficam, respectivamente, assim:

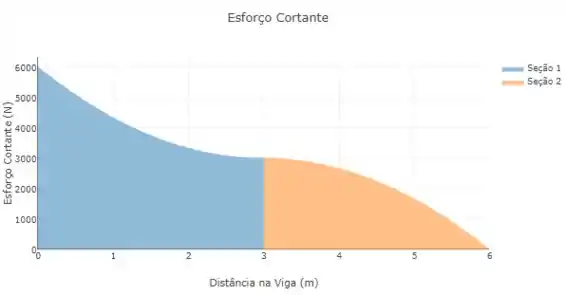
Resposta

Os diagramas de força cortante e momento fletor ficam, respectivamente, assim:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para manter uma porta fechada, é colocada uma ripa entre o piso e a maçaneta. A ripa exerce em B uma força de 175N dirigida ao longo de A B . Substitua essa força por um sistema força-binário equivale
Duas hastes A B e D E são conectadas por um alavanca B C D como mostrado. Sabendo que a tração na haste A B é 720N , determine (a) a tração da haste D E , (b) a reação em C .
Resolva o problema 4.9 considerando que a carga de 50N é substituida por uma carga de 80N .
Resolva o Problema 4.19, considerando que a = 0,32 m .
Uma haste leve é suportada sem atrito por cavilhas em B e C e apoia sem atrito na parede em A. A força vertical de 480 N é aplicada em D. Determine as reações em A, B e C.