Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 77
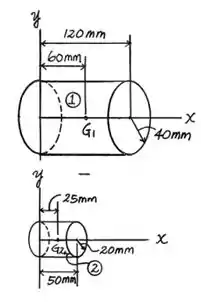
Determine a distância até o centroide do sólido que consiste em um cilindro com um furo de profundidade escavado em sua base.
Passo 1
O problema quer que a gente encontre o centroide , mas como o corpo é formado por um cilindro maior de volume e retirando um cilindro menor de volume .
Passo 2
Primeiro gente vai pegar o valor do centroide em um cilindro, você pode achar eles na internet, mas também fica no final do livro, nele a gente encontra que o centroide é:
Passo 3
Agora, vamos calcular os volumes dos cilindros, também pode ser encontrado no final do livro, então, vamos lá:
Então, agora vamos calcular o centróide resultante:
Resposta
Exercícios de Livros Relacionados
Localize o centro de gravidade x ¯ , y ¯ , z ¯ do arame homogêneo.
O conjunto de placas de aço e alumínio é parafusado e preso ao muro. Cada placa tem uma largura constante na direção z de 200m m e espessura de 20 mm. Se a densidade de A e B é ρ a ç o = 7,85
Uma estrutura de alumínio possui uma seção transversal conhecida como “chapéu fundo”. Localize o centroide y - de sua área. Cada segmento tem uma espessura de 10m m .
Localize o centroide y - para a seção transversal da viga.
Oi tudo bem? Vamos resolver este exercício.Queremos a massa e a localização ( x - ,y - ,z - ) do centro de massa G desta placa composta de aço e latão.Para o cálculo da massa, temos que: m = ρ ⋅ V O v