Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 28

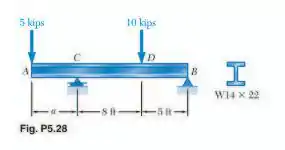
Determine (a) a distância para a qual o valor absoluto do momento de flexão na viga é o menor possível, (b) a correspondente tensão normal máxima em razão da flexão. (veja a sugestão do problema 5.27).

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora praticar mais.

Primeiramente, vamos determinar a reação em B .   Sabemos que:

∑ M C = 0 → 5 a - 8 × 10 + 13 F B = 0

F B = 1 18 80 - 5 a

Não vamos determinar o diagrama de momento fletor neste caso, mas sabemos qual será a cara dele. Sabemos que nas pontas ele será nulo e em C   ele será para cima e em D   para baixo. Ou seja, o momento mínimo e máximo. Usando a dica dada, vamos calcular eles em função de a   e igualar os valores. Fazendo isso:

M C = - 5 a

M D = 5 F B = 5 13 80 - 5 a

Igualando em módulo:

5 a = 5 13 80 - 5 a

Resolvendo e isolando a :

a = 4,44   f t

Passo 2

Agora, basta substituir na fórmula da tensão. O momento máximo, será:

M = 5 a = 5 × 4,44 = 22,2   k i p   i n

Lembre-se de passar de pés para polegadas, pois as propriedades da seção são em polegadas.

M = 22,2   k i p   i n = 266,67   k i p   i n

Sabemos que:

σ = M S

Onde S   é uma propriedade da seção que é tabelada. Para W 14 x 22 ,   temos:

S = 23   i n 3

Ou seja:

σ = M S = 266,67 29 = 9,2   k s i

Resposta

  1. a = 4,44   f t
  2. σ = 9,2   k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão admissível usada no projeto de uma barra de aço é 80M P a . Determine o maior momento M que pode ser aplicado na barra, se: (a) a barra é projetada com entalhes semi-circulares de r = 20m m ,
Uma barra de seção transversal quadrada, como indicado, é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que: (a) ocorra
A barra A B é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que o raio de curvatura da barra seja: (a) 18m
Uma barra de seção transversal quadrada, como indicado, é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 300M P a . Determinar o momento fletor M , para que: (a) ocorra
A barra A B é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que o raio de curvatura da barra seja: (b) 9m