Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 30

Resolva o problema 5.29 considerando P = 480 N e Q = 320 N .

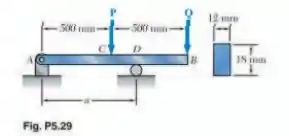
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.

Primeiramente, vamos determinar a reação em A . Sabemos que:

sum M_D = 0 -> - F_A a + 480 (a - 0,5) - 320 ( 1 - a ) = 0

F_A = (800 - (56 0)/(a))

Não vamos determinar o diagrama de momento fletor neste caso, mas sabemos qual será a cara dele. Sabemos que nas pontas ele será nulo e em C ele será para baixo e em D para cima. Ou seja, o momento máximo e mínimo. Usando a dica dada, vamos calcular eles em função de a e igualar os valores. Fazendo isso:

M_C = - 0,5 F_A = - ( 40 0 - (28 0)/(a) )

M_D = - 320 + 320 a

Igualando em módulo:

( 400 - (280)/(a) ) = - 320 + 320 a

320 a^2 + 80 a - 280 = 0

Resolvendo a equação, teremos dois valores para a :

a = 0,8 18 m

a = - 1,06 m

Pegando apenas o positivo:

a = 0,81

Passo 2

Agora, basta substituir na fórmula da tensão. O momento máximo, será:

M = - 320 + 320 a = - 58 N m

Sabemos que:

sigma = (M)/(S)

Onde S é uma propriedade da seção que é igual a (c)/(I) , onde c é a distância da linha neutra e I o momento de inércia. Para este caso, teremos:

S = (1)/(6) b h^2 = 648 xx 10^(- 9) m ³

Ou seja:

sigma = (M)/(S) = (58)/(6,48 xx 10^(- 9)) = 89,5 M P a

Resposta

  1. a = 0,8 1 m
  2. sigma = 89,5 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob 4.80, considerando a viga do Prob 4.79
Resolver o Prob 4.80, considerando a viga do Prob 4.79
Para a viga do Prob 4.76, determinarO momento plástico M p O fator de forma da seção transversal
Para a viga do Prob 4.76, determinarO momento plástico M p O fator de forma da seção transversal
Resolver o Prob 4.80, considerando a viga do Prob 4.77