Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 18
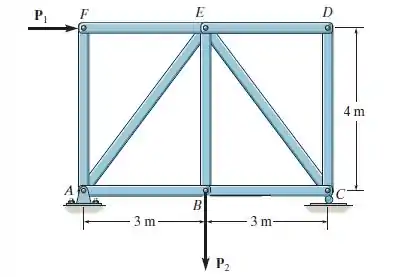
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Considere , .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui um problema em que precisamos determinar a força em cada membro da treliça e indicar se a mesma é de tração ou de compressão.
Relembrando, ao utilizarmos o método dos nós, dizemos que uma força é de compressão quando o sentido da força (a seta) aponta para o nó. Caso contrário, temos uma força de tração.
Bom, vamos começar obtendo as reações e no pino em e no rolete em .
Aplicando as equações de equilíbrio, temos:
Agora que já sabemos as reações, vamos aplicar o método dos nós para cada nó, começando pelo nó !
Passo 2
Então, vamos começar utilizando o método dos nós para o nó . Esboçando o diagrama de equilíbrio, temos:
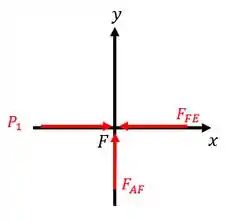
Através das relações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
Passo 3
Vamos seguir agora a nossa análise para o nó . Esboçando o diagrama de equilíbrio, temos:
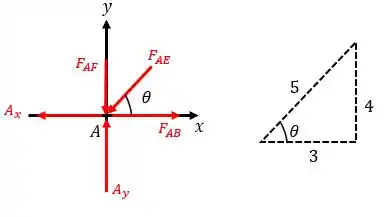
Através das relações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
Passo 4
Vamos seguir agora a nossa análise para o nó . Esboçando o diagrama de equilíbrio, temos:
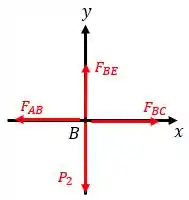
Através das relações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
Passo 5
Vamos seguir agora a nossa análise para o nó . Esboçando o diagrama de equilíbrio, temos:
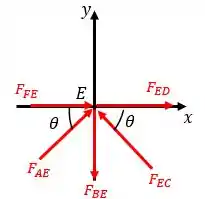
Através das relações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
E por fim, ao fazermos a análise em torno do ponto , obtemos e assim finalizamos a questão!