Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 8
Determine a força cortante e o momento fletor como uma função de , e depois construa os diagramas de força cortante e de momento fletor.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a função da força cortante e do momento fletor. Depois, devemos construir os diagramas de ambos.
Para isto, basta fazermos uma seção a uma distância da extremidade, esboçar o diagrama de corpo livre e aplicar as equações de equilíbrio. Desta forma, vamos começar fazendo o diagrama:
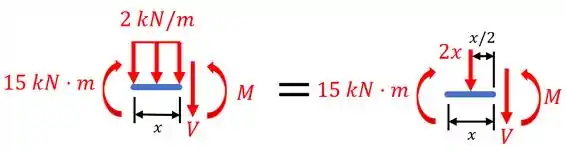
Os dois diagramas acima possuem a mesma informação. A diferença foi que, no diagrama da direita, nós substituímos o carregamento distribuído por uma carga pontual aplicado no meio da distância.
Agora sim, com posse de todas essas informações, vamos as contas!
Passo 2
Para determinarmos as funções da força cortante e do momento fletor, basta aplicarmos as equações de equilíbrio.
Sendo assim, temos:
Resolvendo o sistema acima temos e .
E assim finalizamos a primeira parte da questão!
Passo 3
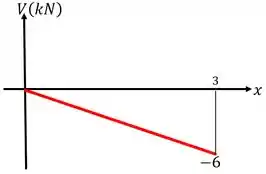
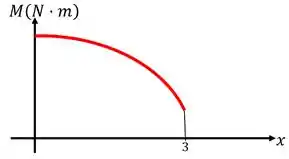
Para finalizarmos a questão, basta esboçarmos os diagramas de força cortante e momento fletor.
Começando pelo diagrama de esforço cortante, temos:
Já o diagrama de momento será:
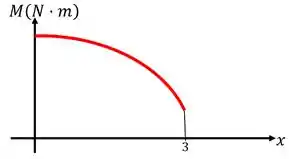
E assim finalizamos a questão!
Resposta
